কিভাবে লেন্স ম্যাগনিফিকেশন গণনা করবেন: 12 টি ধাপ (ছবি সহ)

2024 লেখক: Jason Gerald | [email protected]. সর্বশেষ পরিবর্তিত: 2024-01-16 19:13

অপটিক্যাল যন্ত্রপাতি অধ্যয়ন করার সময়, একটি লেন্সের মতো বস্তুর "বিবর্ধন" হল চিত্রের উচ্চতার অনুপাত যা আপনি বস্তুর প্রকৃত উচ্চতার সাথে দেখতে পান। উদাহরণস্বরূপ, একটি লেন্স যা একটি বস্তুকে খুব বড় দেখাতে পারে তার একটি "উচ্চ" ম্যাগনিফিকেশন ফ্যাক্টর থাকে, যখন একটি লেন্স যা একটি বস্তুকে ছোট দেখায় তার একটি "নিম্ন" ম্যাগনিফিকেশন ফ্যাক্টর থাকে। বস্তুর বর্ধনের সূত্রটি সাধারণত সূত্র ব্যবহার করে গণনা করা হয় এম = (জ_আমি/ঘ_o) = -(ডি_আমি/ডি_o), যেখানে M = বিবর্ধন, h_আমি = ছবির উচ্চতা, জ_o = বস্তুর উচ্চতা, এবং d_আমি এবং ডি_o = ছবি এবং বস্তুর দূরত্ব।

ধাপ

2 এর পদ্ধতি 1: একক লেন্সের বিবর্ধন গণনা করা

নোট: ক কনভার্জিং লেন্স প্রান্তের চেয়ে কেন্দ্রে বিস্তৃত (ম্যাগনিফাইং গ্লাসের মতো)। ক ভিন্ন লেন্স কেন্দ্রের চেয়ে প্রান্তে বিস্তৃত (একটি বাটির মতো)। উভয় লেন্সের বিবর্ধন গণনা একই, সঙ্গে একটি গুরুত্বপূর্ণ ব্যতিক্রম । ডাইভারজেন্ট লেন্সের ব্যতিক্রমগুলিতে সরাসরি যেতে এখানে ক্লিক করুন।

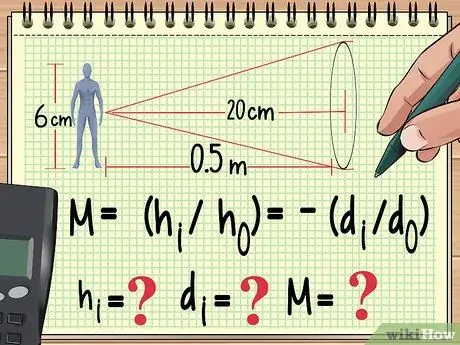
ধাপ 1. আপনার সমীকরণ এবং যে ভেরিয়েবলগুলি আপনি ইতিমধ্যে জানেন তা দিয়ে শুরু করুন।

অন্য যেকোন পদার্থবিজ্ঞানের সমস্যার মতো, একটি বর্ধিত সমস্যা সমাধানের উপায় হল যে সমীকরণটি আপনি গণনা করতে ব্যবহার করবেন। এখান থেকে, আপনি যে সমীকরণটি ব্যবহার করছেন তার থেকে আপনি যে ভেরিয়েবলের মান খুঁজে পাননি তার জন্য আপনি পিছনের দিকে কাজ করতে পারেন।

• উদাহরণস্বরূপ, ধরুন একটি 6 সেমি লম্বা পুতুল a থেকে এক মিটার দূরে রাখা হয়েছে কনভার্জিং লেন্স 20 সেন্টিমিটার ফোকাল দৈর্ঘ্য সহ। যদি আমরা বিবর্ধন, চিত্রের উচ্চতা এবং চিত্রের দূরত্ব গণনা করতে চাই, তাহলে আমরা আমাদের সমীকরণটি লিখতে শুরু করতে পারি:

  এম = (জ_আমি/ঘ_o) = -(ডি_আমি/ডি_o)

• এখন আমরা জানি জ_o (পুতুলের উচ্চতা) এবং d_o (লেন্স থেকে পুতুলের দূরত্ব)। আমরা লেন্সের ফোকাল লেন্থও জানি, যা এই সমীকরণে নেই। আমরা গণনা করব জ_আমি, ঘ_আমি, এবং ম.

ধাপ 2. লেন্স সমীকরণ ব্যবহার করে d_আমি.

আপনি যদি বস্তুর দূরত্ব এবং লেন্সের ফোকাল দৈর্ঘ্য জানেন, তাহলে লেন্স সমীকরণের সাথে গঠিত চিত্র থেকে দূরত্ব গণনা করা খুব সহজ। লেন্সের সমীকরণ হল 1/এফ = 1/ডি_o + 1/ডি_আমি, যেখানে f = লেন্সের ফোকাল দৈর্ঘ্য।

• এই উদাহরণ সমস্যাতে, আমরা লেন্স সমীকরণ ব্যবহার করতে পারি d গণনা করতে_আমি। F এবং d এর মান লিখুন_আমি তারপর সমীকরণটি সমাধান করুন:

  1/এফ = 1/ডি_o + 1/ডি_আমি

  1/20 = 1/50 + 1/ডি_আমি

  5/100 - 2/100 = 1/ডি_আমি

  3/100 = 1/ডি_আমি

  100/3 = ডি_আমি = 33.3 সেমি

• লেন্সের ফোকাল লেন্থ হল লেন্সের কেন্দ্র থেকে সেই বিন্দুর দূরত্ব যেখানে ফোকাল পয়েন্টে আলো সঞ্চারিত হয়। যদি আপনি কখনও পিঁপড়া পোড়ানোর সময় ম্যাগনিফাইং গ্লাস দিয়ে আলোর দিকে মনোনিবেশ করেন তবে আপনি এটি দেখেছেন। পাঠের প্রশ্নে সাধারণত এই হটস্পটের মাত্রা দেওয়া হয়েছে। বাস্তব জীবনে, এই বৈশিষ্ট্যগুলি সাধারণত লেন্সে অবস্থিত একটি লেবেলে লেখা হয়।

ধাপ 3. গণনা জ_আমি.

আপনি গণনা করার পর d_o এবং ডি_আমি, আপনি বিবর্ধিত বস্তুর উচ্চতা এবং লেন্সের বিবর্ধন গণনা করতে পারেন। লেন্সের বিবর্ধন সমীকরণে দুটি সমান চিহ্ন লক্ষ্য করুন (M = (h_আমি/ঘ_o) = -(ডি_আমি/ডি_o)) - এর মানে হল যে এই সমীকরণের সমস্ত অংশ একে অপরের সমান, তাই আমরা M এবং h গণনা করতে পারি_আমি আমরা যে ক্রমে চাই।

• এই উদাহরণ সমস্যার জন্য, আমরা h গণনা করতে পারি_আমি এটার মত:

  (জ_আমি/ঘ_o) = -(ডি_আমি/ডি_o)

  (জ_আমি/6) = -(33, 3/50)

  জ_আমি = -(33, 3/50) x 6

  জ_আমি = - 3, 996 সেমি

• লক্ষ্য করুন যে এখানে বস্তুর উচ্চতা নেতিবাচক যা ইঙ্গিত করে যে আমরা যে ছবিটি পরে দেখব তা উল্টে যাবে (উপরে-নীচে)।

ধাপ 4. এম গণনা করা

আপনি সমীকরণ দিয়ে শেষ পরিবর্তনশীল গণনা করতে পারেন -(d_আমি/ডি_o) অথবা (জ_আমি/ঘ_o).

• নিম্নলিখিত উদাহরণে, কিভাবে এম গণনা করা যায় তা নিম্নরূপ:

  এম = (জ_আমি/ঘ_o)

  এম = (-3, 996/6) = - 0, 666

• D এর মান ব্যবহার করে গণনা করলে ফলাফলও একই হবে:

  এম = -(ডি_আমি/ডি_o)

  এম = -(33, 3/50) = - 0, 666

• লক্ষ্য করুন যে জুমের একটি ইউনিট লেবেল নেই।

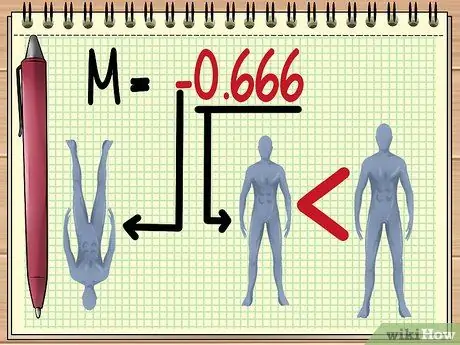
ধাপ 5. এম মান বোঝা।

একবার আপনি এম মানের মাত্রা পেয়ে গেলে, আপনি লেন্সের মাধ্যমে যে ছবিটি দেখতে পাবেন সে সম্পর্কে আপনি বেশ কিছু জিনিস অনুমান করতে পারেন, যথা:

• আকার.

  এম এর "পরম মান" যত বড় হবে, লেন্স দিয়ে দেখা বস্তুটি তত বড় হবে। 0 থেকে 1 এর মধ্যে M মান নির্দেশ করে যে বস্তুটি ছোট দেখাবে।

• অবজেক্ট ওরিয়েন্টেশন।

  একটি নেতিবাচক মান নির্দেশ করে যে গঠিত চিত্রটি বিপরীত হবে।

• এখানে দেওয়া উদাহরণে, -0.666 এর M মান মানে, বিদ্যমান চলকের মান অনুযায়ী পুতুলের ছায়া দৃশ্যমান হবে। উল্টো এবং প্রকৃত আকারের চেয়ে দুই তৃতীয়াংশ ছোট.

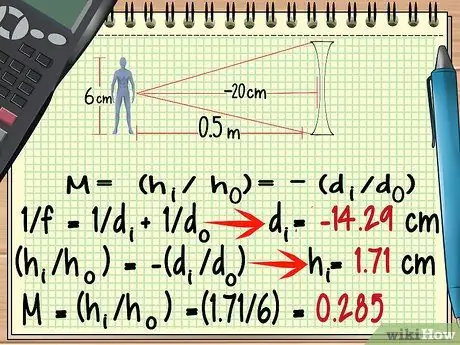
পদক্ষেপ 6. একটি ডাইভারজিং লেন্সের জন্য, একটি নেতিবাচক ফোকাল পয়েন্ট ব্যবহার করুন।

যদিও একটি ডাইভারজিং লেন্সের আকৃতি একটি কনভার্জিং লেন্সের থেকে অনেকটা আলাদা, আপনি উপরের মত একই সূত্র ব্যবহার করে এর বর্ধিতকরণ গণনা করতে পারেন। মনে রাখার ব্যতিক্রমগুলি হল ডাইভারজিং লেন্সের ফোকাল পয়েন্ট নেগেটিভ।

উপরের উদাহরণের সমস্যাটিতে, এটি উত্তর গণনা করতে আপনি যে উত্তর পাবেন তা প্রভাবিত করবে_আমি, তাই নিশ্চিত করুন যে আপনি এই দিকে মনোযোগ দিন।

• আসুন উপরের উদাহরণের সমস্যাটি পুনরায় কাজ করি, শুধুমাত্র এখন আমরা ফোকাল দৈর্ঘ্যের একটি ডাইভারজিং লেন্স ব্যবহার করি - 20 সেমি

  অন্যান্য ভেরিয়েবল একই মান থাকে।

• প্রথমত, আমরা গণনা করব d_আমি লেন্স সমীকরণ ব্যবহার করে:

  1/এফ = 1/ডি_o + 1/ডি_আমি

  1/-20 = 1/50 + 1/ডি_আমি

  -5/100 - 2/100 = 1/ডি_আমি

  -7/100 = 1/ডি_আমি

  -100/7 = ডি_আমি = - 14, 29 সেমি

• এখন আমরা h গণনা করব_আমি এবং d এর মান সহ M_আমি নতুন একটি.

  (জ_আমি/ঘ_o) = -(ডি_আমি/ডি_o)

  (জ_আমি/6) = -(-14, 29/50)

  জ_আমি = -(-14, 29/50) x 6

  জ_আমি = 1, 71 সেমি

  এম = (জ_আমি/ঘ_o)

  এম = (1, 71/6) = 0, 285

2 এর পদ্ধতি 2: একাধিক লেন্সের বিবর্ধন গণনা করা

সহজ দুই লেন্স পদ্ধতি

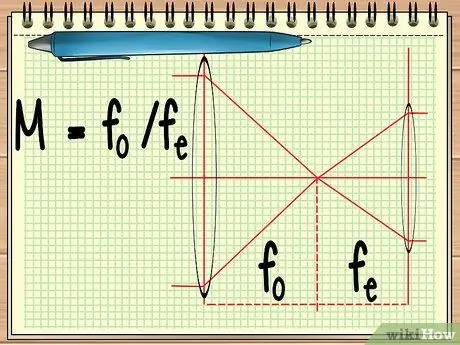
ধাপ 1. দুটি লেন্সের কেন্দ্রবিন্দু গণনা করুন।

যখন আপনি একটি যন্ত্র ব্যবহার করেন যা দুটি লেন্সের পাশাপাশি সাজানো থাকে (যেমন একটি টেলিস্কোপ বা দূরবীন) এটি সহজ সমীকরণ M = f দ্বারা গণনা করা যেতে পারে_o/চ_ই.

সমীকরণে, চ_o বস্তুনিষ্ঠ লেন্সের কেন্দ্রবিন্দু এবং f_ই আইপিসের কেন্দ্রবিন্দু। অবজেক্টিভ লেন্স হল বস্তুর কাছাকাছি থাকা বড় লেন্স, যখন অকুলার লেন্স হল লেন্স যা পর্যবেক্ষকের চোখের কাছাকাছি অবস্থিত।

ধাপ 2. আপনার কাছে ইতিমধ্যেই থাকা তথ্য M = f সমীকরণে প্লাগ করুন_o/চ_ই.

একবার আপনার উভয় লেন্সের ফোকাল পয়েন্ট থাকলে, সেগুলি গণনা করা খুব সহজ, - আইপিসের ফোকাল লেন্থের ফোকাল লেন্থের ফোকাল লেন্থকে ভাগ করে অনুপাত গণনা করুন। আপনি যে উত্তরটি পান তা হল টুলের মোট পরিবর্ধন।

• উদাহরণস্বরূপ, ধরুন একটি সাধারণ টেলিস্কোপ, এটি লেখা আছে যে অবজেক্টিভ লেন্সের ফোকাল পয়েন্ট 10 সেমি এবং আইপিসের ফোকাল পয়েন্ট 5 সেমি, তারপর বর্ধিতকরণ 10/5 = 2.

  জটিল পদ্ধতি

  

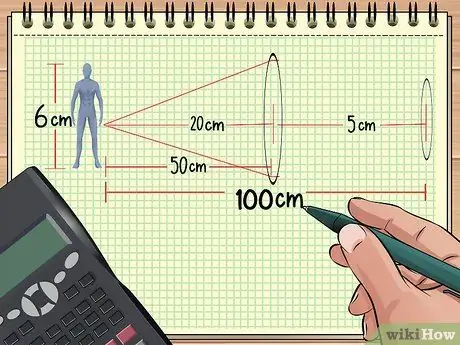
  ধাপ 1. লেন্স এবং বস্তুর মধ্যে দূরত্ব গণনা করুন।

  যদি আপনার কোন বস্তুর সামনে একটি সারিতে দুটি লেন্স সাজানো থাকে, তাহলে লেন্স থেকে বস্তুর দূরত্ব, বস্তুর আকার এবং দুটি লেন্সের কেন্দ্রবিন্দু জানলে মোট পরিবর্ধন গণনা করা যাবে। বাকিটাও গণনা করা যায়।

  উদাহরণস্বরূপ, ধরুন আমরা উপরের উদাহরণ 1 এর মতো বস্তু এবং লেন্সগুলি সাজাই: একটি পুতুল একটি কনভার্জিং লেন্স থেকে 50 সেমি, যার ফোকাল দৈর্ঘ্য 20 সেমি। এখন, প্রথম লেন্স থেকে 50 সেমি (পুতুল থেকে 100 সেমি।) এর ফোকাল পয়েন্ট 5 সেমি দিয়ে দ্বিতীয় লেন্সটি রাখুন, এর পরে, আমরা প্রাপ্ত তথ্য ব্যবহার করে মোট বর্ধন গণনা করব।

  

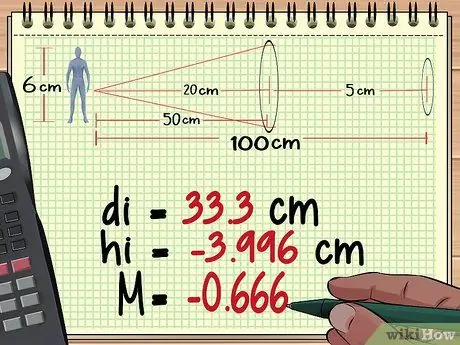
  ধাপ 2. লেন্স 1 থেকে বস্তুর দূরত্ব, উচ্চতা এবং বিবর্ধন গণনা করুন।

  একাধিক লেন্সের বিবর্ধন গণনার প্রথম অংশটি একটি একক লেন্সের বিবর্ধন গণনার সমান। বস্তুর সবচেয়ে কাছের লেন্স দিয়ে শুরু করুন, লেন্স সমীকরণ ব্যবহার করে তৈরি হওয়া ছবি থেকে দূরত্ব বের করুন, তারপর ছবির উচ্চতা এবং পরিবর্ধন খুঁজে বের করার জন্য বিবর্ধন সমীকরণ ব্যবহার করুন। আরো একক লেন্স বিবর্ধন গণনা দেখতে এখানে ক্লিক করুন।

  • উপরের পদ্ধতি 1 এ আমাদের গণনা থেকে, আমরা দেখতে পাই যে প্রথম লেন্সটি একটি উচ্চতর চিত্র তৈরি করে - 3, 996 সেমি, দূরত্ব 33.3 সেমি লেন্সের পিছনে, এবং - 0, 666.

    

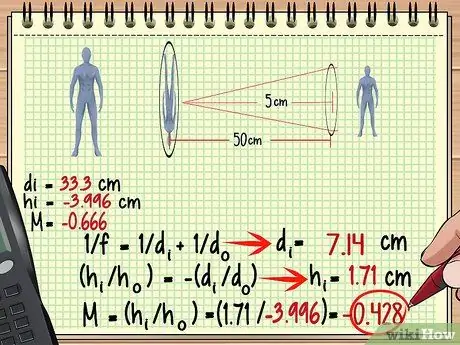
    ধাপ the। প্রথম লেন্সের ছবিটি দ্বিতীয় লেন্সের বস্তু হিসেবে ব্যবহার করুন।

    এখন, দ্বিতীয় লেন্সের জন্য পরিবর্ধন, উচ্চতা এবং আরও অনেক কিছু খুঁজে পাওয়া খুব সহজ - আপনি যে পদ্ধতিটি প্রথম লেন্সের জন্য ব্যবহার করেছিলেন, সেই পদ্ধতিটিই ব্যবহার করুন, শুধুমাত্র, এই সময় ছবিটিকে একটি বস্তু হিসেবে বিবেচনা করুন। মনে রাখবেন যে দ্বিতীয় লেন্সের ছবির দূরত্ব সর্বদা প্রথম লেন্সের বস্তুর দূরত্বের মতো নয়।

    • উপরের উদাহরণে, যেহেতু ছবিটি প্রথম লেন্সের পিছনে 33.3 সেমি গঠিত, তাই দূরত্ব 50-33.3 = 16.7 সেমি দ্বিতীয় লেন্সের সামনে। আসুন এই পরিমাপ এবং দ্বিতীয় লেন্সের ফোকাল দৈর্ঘ্য ব্যবহার করে দ্বিতীয় লেন্স দ্বারা গঠিত ছবিটি খুঁজে বের করি।

      1/এফ = 1/ডি_o + 1/ডি_আমি

      1/5 = 1/16, 7 + 1/ডি_আমি

      0, 2 - 0, 0599 = 1/ডি_আমি

      0, 14 = 1/ডি_আমি

      ঘ_আমি = 7, 14 সেমি

    • এখন আমরা h গণনা করতে পারি_আমি এবং দ্বিতীয় লেন্সের জন্য M:

      (জ_আমি/ঘ_o) = -(ডি_আমি/ডি_o)

      (জ_আমি/-3, 996) = -(7, 14/16, 7)

      জ_আমি = -(0, 427) x -3, 996

      জ_আমি = 1, 71 সেমি

      এম = (জ_আমি/ঘ_o)

      এম = (1, 71/-3, 996) = - 0, 428

    

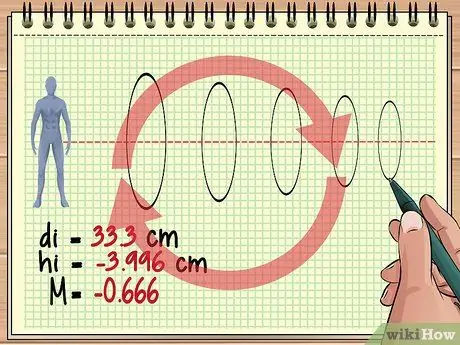
    ধাপ 4. অতিরিক্ত লেন্সের জন্য এভাবে গণনা চালিয়ে যান।

    এই মৌলিক পদ্ধতি একই যদি তিনটি, চার, বা শত শত লেন্স একটি বস্তুর সামনে সারিবদ্ধ থাকে। প্রতিটি লেন্সের জন্য, পূর্ববর্তী লেন্সের ছবিটিকে বস্তু হিসেবে বিবেচনা করুন এবং লেন্স সমীকরণ এবং বিবর্ধন সমীকরণ ব্যবহার করুন যাতে আপনি আপনার উত্তর চান।

    মনে রাখবেন যে প্রতিটি পরবর্তী লেন্স ক্রমাগত গঠিত চিত্রকে উল্টাতে পারে। উদাহরণস্বরূপ, আমরা পূর্বে প্রাপ্ত ম্যাগনিফিকেশন ভ্যালু (-0, 428) নির্দেশ করে যে আমরা যে ছবিটি দেখতে যাচ্ছি তা প্রকৃত বস্তুর আকারের প্রায় 4/10, কিন্তু লম্ব, কারণ আগের লেন্সের ছবিটি উল্টানো।

    পরামর্শ

    • বাইনোকুলার সাধারণত একটি সংখ্যাকে অন্য সংখ্যার আকারে বিবর্ধন বৈশিষ্ট্যের ব্যাখ্যা প্রদান করে। উদাহরণস্বরূপ, দূরবীন 8x25 বা 8x40 হিসাবে নির্দিষ্ট করা যেতে পারে। যখন এরকম লেখা হয়, প্রথম সংখ্যাটি হল বাইনোকুলার এর বিবর্ধন। প্রদত্ত উদাহরণের মধ্যেও কোন ব্যাপার নেই, দুটি সংখ্যা মাত্রায় ভিন্ন, উভয় বাইনোকুলারের 8 গুণ বড় করা আছে দ্বিতীয় সংখ্যাটি ইঙ্গিত দেয় যে বাইনোকুলার দ্বারা ছবিটি কতটা পরিষ্কার হবে।
    • মনে রাখবেন যে একক লেন্সের লুপের জন্য, বস্তুর দূরত্ব লেন্সের ফোকাল দৈর্ঘ্যের চেয়ে বেশি হলে বর্ধিতকরণ নেতিবাচক হবে। এর অর্থ এই নয় যে গঠিত চিত্রটি ছোট হবে। এই ক্ষেত্রে, বর্ধন এখনও ঘটে, কিন্তু গঠিত চিত্রটি পর্যবেক্ষক দ্বারা উল্টো (উপরে-নিচে) দেখা যাবে।