আপনি কি ক্যালকুলেটর ব্যবহার না করে রৈখিক সমীকরণ আঁকতে জানেন না? ভাগ্যক্রমে, রৈখিক সমীকরণগুলি গ্রাফ করা মোটামুটি সহজ যদি আপনি জানেন। আপনাকে শুধু আপনার সমীকরণ সম্পর্কে কয়েকটি বিষয় বুঝতে হবে এবং আপনি এটি করতে সক্ষম হবেন। চল শুরু করি.
ধাপ
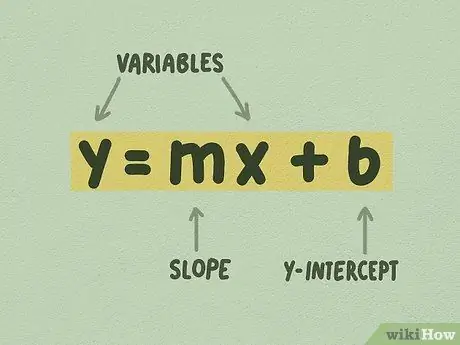
ধাপ 1. নিশ্চিত করুন যে রৈখিক সমীকরণটি y = mx + b রূপ আছে।
এই আকৃতিটিকে বলা হয় y- ইন্টারসেপ্ট ফর্ম, এবং সম্ভবত গ্রাফ রৈখিক সমীকরণ ব্যবহার করার জন্য এটি সবচেয়ে সহজ ফর্ম। সমীকরণের মান একটি পূর্ণসংখ্যা হতে হবে না। প্রায়শই, আপনি একটি সমীকরণ দেখতে পাবেন যা এইরকম: y = 1/4x + 5, যেখানে 1/4 হল m এবং 5 হল b।
- m কে "opeাল" বা কখনও কখনও "গ্রেডিয়েন্ট" বলা হয়। Opeালটি পাশের বৃদ্ধি, অথবা y- এর পরিবর্তনকে x- এর পরিবর্তনের দ্বারা বিভক্ত হিসাবে সংজ্ঞায়িত করা হয়।
- b কে "y-intercept" হিসাবে সংজ্ঞায়িত করা হয়েছে। ওয়াই-ইন্টারসেপ্ট হল সেই বিন্দু যেখানে লাইনটি Y- অক্ষকে ছেদ করে।
- x এবং y ভেরিয়েবল। আপনি একটি নির্দিষ্ট x মানের জন্য সমাধান করতে পারেন, উদাহরণস্বরূপ, যদি আপনার y বিন্দু থাকে এবং m এবং b এর মানগুলি জানেন। যাইহোক, x, এর শুধুমাত্র একটি মান নেই: লাইনটি উপরে বা নিচে যাওয়ার সাথে সাথে এর মান পরিবর্তিত হয়।
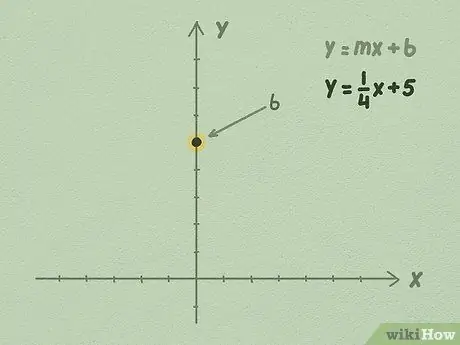
ধাপ 2. Y অক্ষের উপর b সংখ্যাটি আঁকুন।
আপনার b মান সর্বদা একটি মূলদ সংখ্যা হবে। সংখ্যা b যাই হোক না কেন, Y অক্ষে এর মান খুঁজুন এবং উল্লম্ব অক্ষের একটি বিন্দুতে সংখ্যাটি রাখুন।
উদাহরণস্বরূপ, আসুন y = 1/4x + 5 সমীকরণটি ব্যবহার করি। যেহেতু শেষ সংখ্যাটি b, তাই আমরা জানি যে b হল 5 এর সমান। এখানেই আপনার সরলরেখা Y অক্ষকে ছেদ করবে।
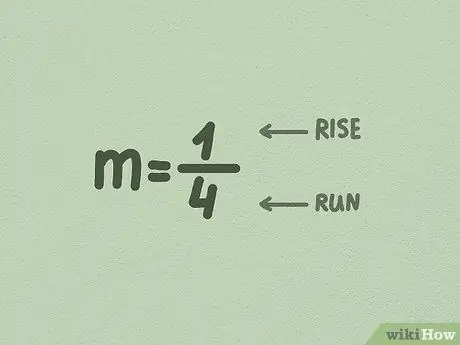
ধাপ 3. m কে ভগ্নাংশে রূপান্তর করুন।
প্রায়শই, x এর সামনে সংখ্যাটি ইতিমধ্যে একটি ভগ্নাংশ, তাই আপনাকে এটি পরিবর্তন করতে হবে না। কিন্তু যদি না হয়, তবে 1 এর নীচে m এর মান রেখে এটি পরিবর্তন করুন।
- প্রথম সংখ্যা (সংখ্যার) হল আরোহণের বৃদ্ধি যা পাশে ভাগ করা হয়। এই সংখ্যাটি নির্দেশ করে যে লাইনটি কতদূর যায়, বা উল্লম্বভাবে।
- দ্বিতীয় সংখ্যাটি (হর) হল আরোহণের দিকটি পাশ দিয়ে ভাগ করা। এই সংখ্যাটি নির্দেশ করে যে লাইনটি কতদূর সরে যায়, বা অনুভূমিকভাবে।
- উদাহরণ স্বরূপ:
- 4/1 এর opeাল প্রতি 1 পয়েন্টের জন্য 4 পয়েন্ট উপরে নিয়ে যায়।
- -2/1 এর opeাল প্রতি 1 পয়েন্টের জন্য 2 পয়েন্ট নিচে সরে যায়।
- 1/5 এর opeাল প্রতি 5 পয়েন্টের জন্য 1 পয়েন্ট উপরে চলে যায়।
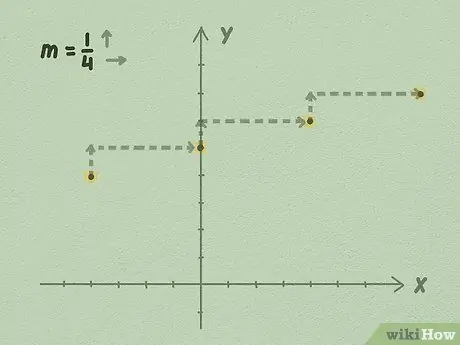
ধাপ 4. bাল ব্যবহার করে লাইনটি প্রসারিত করা শুরু করুন, অথবা পাশে ভাগ করে উপরে।
আপনার b মান দিয়ে শুরু করুন: আমরা জানি যে সমীকরণটি এই বিন্দুতে চলে গেছে। আপনার opeাল নিয়ে এবং সমীকরণে পয়েন্ট পেতে তার মান ব্যবহার করে লাইনটি প্রসারিত করুন।
- উদাহরণস্বরূপ, উপরের চিত্রটি ব্যবহার করে, আপনি দেখতে পারেন যে প্রতি 1 পয়েন্টের জন্য, লাইনটি 4 পয়েন্ট ডানদিকে চলে যায়। এটি ঘটে কারণ লাইনের opeাল 1/4। আপনি লাইনটি অনির্দিষ্টকালের জন্য উভয় দিকে প্রসারিত করেন, লাইনটি গ্রাফ করার জন্য পাশে ভাগ করে ব্যবহার করা চালিয়ে যান।
- উপরে উঠার সময় opeাল ইতিবাচক, এবং নিচে movingাল নেতিবাচক। উদাহরণস্বরূপ -1/4 এর opeাল, প্রতি 4 পয়েন্টের জন্য 1 পয়েন্ট নিচে সরে যাবে।
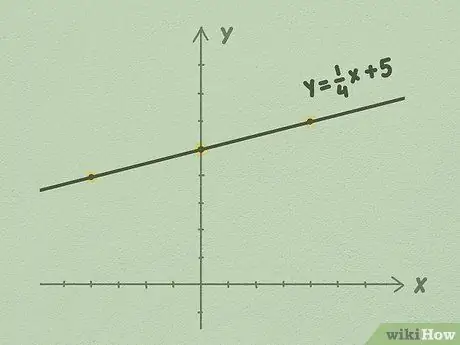
ধাপ 5. লাইন প্রসারিত করা চালিয়ে যান, একটি রুলার ব্যবহার করে এবং mাল, m, একটি গাইড হিসাবে ব্যবহার নিশ্চিত করুন।
অনির্দিষ্টকালের জন্য লাইনটি প্রসারিত করুন এবং আপনি আপনার রৈখিক সমীকরণ গ্রাফিং সম্পন্ন করেছেন। বেশ সহজ, তাই না?
