- লেখক Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- সর্বশেষ পরিবর্তিত 2025-01-23 12:07.
পদার্থবিজ্ঞানে স্থানচ্যুতি কোনো বস্তুর অবস্থানের পরিবর্তনকে নির্দেশ করে। যখন আপনি স্থানচ্যুতি গণনা করেন, আপনি একটি বস্তুর প্রাথমিক এবং চূড়ান্ত অবস্থানের উপর ভিত্তি করে কতটা দূরে তা গণনা করেন। স্থানচ্যুতি গণনা করার জন্য আপনি যে সূত্রটি ব্যবহার করেন তা সমস্যার প্রদত্ত পরিবর্তনশীলতার উপর নির্ভর করে। স্থানচ্যুতি গণনা করতে এই পদক্ষেপগুলি অনুসরণ করুন।
ধাপ
5 এর অংশ 1: ফলস্বরূপ স্থানচ্যুতি গণনা করা

ধাপ ১. ফলে দূরত্বের এককটি আপনার শুরু এবং শেষের অবস্থান নির্দেশ করতে ব্যবহৃত হলে ফলস্বরূপ স্থানচ্যুতি সূত্রটি ব্যবহার করুন।
যদিও দূরত্ব স্থানচ্যুতি থেকে আলাদা, ফলস্বরূপ স্থানচ্যুতি সমস্যাটি কত কিলোমিটার বা মিটার ভ্রমণ করেছে তা সন্ধান করে। আপনি পরিমাপের এই এককটি ব্যবহার করে স্থানচ্যুতি গণনা করবেন এবং কোন বস্তুর অবস্থান তার শুরু বিন্দু থেকে কতটা দূরে সরে যায়।
- ফলস্বরূপ স্থানচ্যুতি সূত্রটি লেখা হয়েছে: S = x²+y² । S হল স্থানচ্যুতি। X হল বস্তুর গতির প্রথম দিক এবং Y হল বস্তুর গতির দ্বিতীয় দিক। যদি আপনার বস্তু শুধুমাত্র এক দিকে চলে, তাহলে Y = 0।
- একটি বস্তু শুধুমাত্র সর্বোচ্চ দুটি দিকে চলাচল করতে পারে কারণ উত্তর/দক্ষিণ অথবা পূর্ব/পশ্চিম অক্ষ বরাবর চলাকে নিরপেক্ষ গতি বলে মনে করা হয়।

ধাপ ২. বিন্দুগুলিকে গতির ক্রমে সংযুক্ত করুন এবং সেগুলিকে A-Z থেকে লেবেল করুন।
বিন্দু থেকে বিন্দুতে সরলরেখা আঁকতে শাসক ব্যবহার করুন।
- এছাড়াও একটি সরল রেখা ব্যবহার করে আপনার প্রারম্ভিক বিন্দুকে আপনার শেষ বিন্দুর সাথে সংযুক্ত করতে মনে রাখবেন। এই স্থানচ্যুতি আমরা গণনা করব।
- উদাহরণস্বরূপ, যদি কোন বস্তু পূর্ব দিকে 300 মিটার এবং উত্তর 400 মিটার সরে যায়, তাহলে এটি একটি সমকোণী ত্রিভুজ গঠন করবে। AB হবে ত্রিভুজের প্রথম লেগ, আর BC হবে দ্বিতীয় লেগ। এসি ত্রিভুজের হাইপোটেনিউজ হবে এবং এর মাত্রা বস্তুর স্থানচ্যুতি। এই উদাহরণে, দুটি দিক পূর্ব এবং উত্তর।

ধাপ 3. x² এবং y²- এর মান লিখুন।
এখন যেহেতু আপনি আপনার বস্তুর গতির দুটি দিক জানেন, মানগুলি যথাযথ ভেরিয়েবলে প্রবেশ করুন।
উদাহরণস্বরূপ, x = 300 এবং y = 400. আপনার সূত্র এইরকম হওয়া উচিত: S = 300² + 400²।
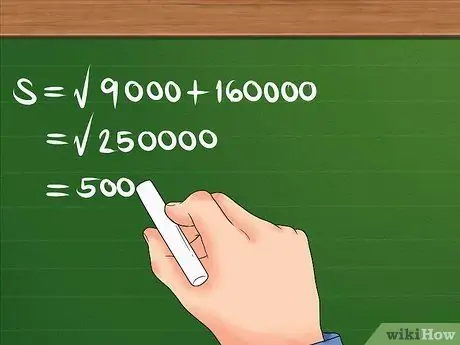
পদক্ষেপ 4. অপারেশন ক্রম ব্যবহার করে সূত্র গণনা করুন।
স্কয়ার 300 এবং 400 প্রথমে, তারপর তাদের যোগ করুন, এবং যোগফল এর বর্গমূল খুঁজুন।
উদাহরণস্বরূপ: S = 90000 + 160000. S = 250000। S = 500. এখন আপনি জানেন যে স্থানচ্যুতি 500 মি।
5 এর অংশ 2: যখন গতি এবং সময় জানা যায়

ধাপ 1. এই সূত্রটি ব্যবহার করুন যখন সমস্যাটি আপনাকে কোন বস্তুর গতি এবং সময় লাগে।
কিছু গণিত সমস্যা আপনাকে বলবে না কোন বস্তু কতদূর বা কত দ্রুত এগিয়ে যাচ্ছে। আপনি সময় এবং গতির এই মাত্রা ব্যবহার করে স্থানচ্যুতি গণনা করতে পারেন।
-
এই ক্ষেত্রে, সূত্র হয়ে যায়: S = 1/2 (u + v) t।
U = বস্তুর প্রাথমিক বেগ, বা বস্তু কত দ্রুত গতিতে একটি নির্দিষ্ট দিকে যেতে শুরু করে। V = বস্তুর চূড়ান্ত বেগ, বা বস্তু তার চূড়ান্ত অবস্থানের দিকে কত দ্রুত এগিয়ে যাচ্ছে। T = বস্তুকে তার চূড়ান্ত স্থানে পৌঁছাতে সময় লাগে।
- উদাহরণ: একটি গাড়ি 45 সেকেন্ডের জন্য রাস্তায় নেমে যায় (সময় প্রয়োজন)। গাড়ী পশ্চিম দিকে ঘুরছে 20 m/s (প্রাথমিক গতি) এবং রাস্তার শেষে, এর গতি 23 m/s (চূড়ান্ত গতি)। এই কারণগুলির উপর ভিত্তি করে স্থানচ্যুতি গণনা করুন।

ধাপ 2. যথাযথ ভেরিয়েবলে প্রয়োজনীয় গতি এবং সময় লিখুন।
এখন যেহেতু আপনি জানেন যে গাড়ি কতদূর এগোচ্ছে, গাড়ি শুরু এবং শেষের দিকে কত দ্রুত এগিয়ে যাচ্ছে, আপনি শুরু করার স্থান থেকে চূড়ান্ত অবস্থানের দূরত্ব খুঁজে পেতে পারেন।
আপনার সূত্র এই মত হওয়া উচিত: S = 1/2 (20 + 23) 45।

ধাপ 3. সঠিক জায়গায় মান রাখার পর সূত্র গণনা করুন।
ক্রিয়াকলাপের ক্রম অনুসরণ করতে মনে রাখবেন, অন্যথায় স্থানচ্যুতিগুলি খুব ভিন্ন মান নিয়ে আসবে।
- এই সূত্রের জন্য, আপনি যদি ঘটনাক্রমে শুরু এবং শেষের গতি অদলবদল করেন তবে এটি কোন ব্যাপার নয়। যেহেতু আপনি প্রথমে এই সংখ্যাগুলিকে একসাথে যুক্ত করবেন, সেগুলি বন্ধনীতে কোথায় আছে তা বিবেচ্য নয়। যাইহোক, অন্যান্য সূত্রের জন্য, প্রাথমিক এবং চূড়ান্ত বেগের অদলবদলের ফলে বিভিন্ন স্থানচ্যুতি মান হবে।
- আপনার সূত্রটি এইরকম হওয়া উচিত: S = 1/2 (43) 45। প্রথমে 43 কে 2 দিয়ে ভাগ করুন, যার ফলাফল 21, 5। তারপর 21, 5 কে 45 দিয়ে গুণ করুন, ফলে ফলাফল 967.5 মিটার। 967, 5 হল আপনার স্থানচ্যুতের মাত্রা, অথবা আপনার গাড়ি তার প্রারম্ভিক স্থান থেকে কতদূর অগ্রসর হয়েছে।
5 এর 3 ম অংশ: যখন প্রাথমিক বেগ, ত্বরণ, এবং সময় জানা যায়
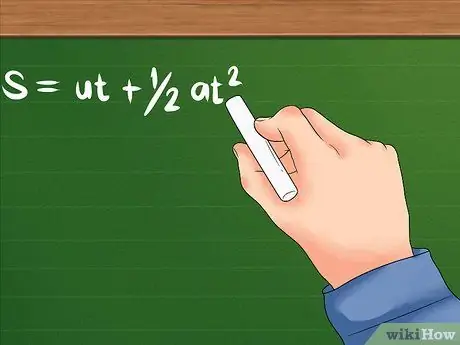
ধাপ 1. প্রাথমিক বেগ এবং সময় ছাড়াও ত্বরণ জানা গেলে পরিবর্তিত সূত্রটি ব্যবহার করুন।
কিছু প্রশ্ন কেবল আপনাকে বলবে যে বস্তুটি শুরুতে কত দ্রুত গতিতে চলছে, বস্তুটি কত দ্রুত গতিতে শুরু করছে এবং বস্তুটি কতদূর এগিয়ে যাচ্ছে। আপনি নিম্নলিখিত সূত্র প্রয়োজন হবে।
- এই সমস্যার সূত্র হল: S = ut + 1/2at² । U এখনও প্রাথমিক গতি নির্দেশ করে; a হচ্ছে বস্তুর ত্বরণ, বা তার বেগ কত দ্রুত পরিবর্তন হতে শুরু করে। T এর অর্থ হতে পারে সময় বা নির্দিষ্ট পরিমাণে কোন বস্তুকে ত্বরান্বিত করতে লাগে। উভয়ই সময় ইউনিট যেমন সেকেন্ড, ঘন্টা এবং অন্যান্য ব্যবহার করবে।
- ধরুন একটি গাড়ি 25 m/s (প্রাথমিক বেগ) এ চলতে শুরু করে 3 m/s2 (ত্বরণ) 4 সেকেন্ডের (সময়) গতিতে ত্বরান্বিত হতে শুরু করে। 4 সেকেন্ড পরে গাড়ির স্থানচ্যুতি কত?

ধাপ 2. সূত্রে মান লিখুন।
পূর্ববর্তী সূত্রের বিপরীতে, এখানে শুধুমাত্র প্রাথমিক গতি উপস্থাপন করা হয়, তাই সঠিক ডেটা লিখতে ভুলবেন না।
উপরের নমুনা ডেটার উপর ভিত্তি করে, আপনার সূত্রটি এইরকম হবে: S = 25 (4) + 1/2 (3) 4²। এটি আপনার ত্বরণের মাত্রা এবং সময়ের চারপাশে বন্ধনী যোগ করতে সাহায্য করে যাতে আপনি সংখ্যাগুলিকে আলাদা করতে পারেন।
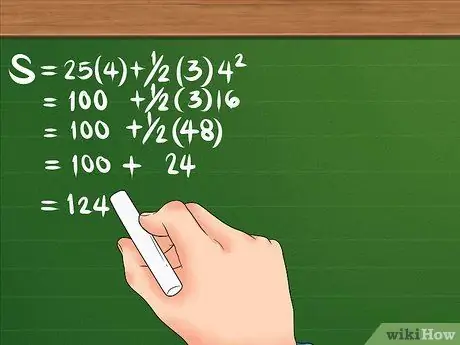
পদক্ষেপ 3. অপারেশনের সঠিক ক্রমে এটি স্থানচ্যুতি গণনা করুন।
ক্রিয়াকলাপের ক্রম মনে রাখতে আপনাকে সাহায্য করার একটি দ্রুত উপায় হল গাধা সেতু কুড় ইর কুয়া সি কাদং বা ওয়া জুরাগান কচ্ছপ। এটি সঠিক ক্রমকে উপস্থাপন করে: বন্ধনী, বর্গ, গুণ, ভাগ, যোগ, এবং বিয়োগ।
আসুন সূত্রটি আবার দেখি: S = 25 (4) + 1/2 (3) 4²। প্রথম, বর্গ 4, ফলাফল হল 16. তারপর, 16 কে 3 দিয়ে গুণ করুন, 48 তৈরি করুন; তারপর 100 করতে 25 কে 4 দিয়ে গুন করুন।
5 এর 4 ম অংশ: কৌণিক স্থানচ্যুতি গণনা করা

ধাপ 1. কৌণিক স্থানচ্যুতি খুঁজুন যখন বস্তুটি বৃত্তাকার পথে চলে।
যদিও আপনি এখনও একটি সরলরেখা ব্যবহার করে স্থানচ্যুতি গণনা করবেন, বস্তুর শুরু এবং শেষ অবস্থানের মধ্যে পার্থক্যটি খুঁজে বের করতে হবে কারণ এটি একটি বৃত্তাকার পথে চলে।
- কল্পনা করুন যে একটি মেয়ে আনন্দ-উল্লাসে বসে আছে। যখন সে ক্যারোজেলের সাথে ঘুরবে, সে বৃত্তাকার পথে চলবে। কৌণিক স্থানচ্যুতি প্রাথমিক এবং চূড়ান্ত অবস্থানের মধ্যে স্বল্পতম দূরত্ব খুঁজে বের করার চেষ্টা করে যখন বস্তুটি সরলরেখায় চলে না।
- কৌণিক স্থানচ্যুতি জন্য সূত্র হল: = এস/আর, যেখানে S হল রৈখিক স্থানচ্যুতি, r হল ব্যাসার্ধ, এবং কৌণিক স্থানচ্যুতি। রৈখিক স্থানচ্যুতি হল কোন বস্তু একটি চাপের সাথে কতদূর অগ্রসর হয়। ব্যাসার্ধ হল বৃত্তের কেন্দ্রে বস্তুর দূরত্ব। কৌণিক স্থানচ্যুতি হল সেই মান যা আমরা খুঁজে পেতে চাই।

ধাপ 2. সমীকরণের মধ্যে রৈখিক স্থানচ্যুতি এবং ব্যাসার্ধ প্লাগ করুন।
মনে রাখবেন যে ব্যাসার্ধ হল বৃত্তের কেন্দ্র থেকে দূরত্ব; কিছু সমস্যা আপনাকে একটি বৃত্তের ব্যাস বলবে, যা ব্যাসার্ধ খুঁজে পেতে 2 দ্বারা ভাগ করা আবশ্যক।
- এখানে একটি উদাহরণ সমস্যা: একটি মেয়ে একটি আনন্দদায়ক ঘোরাঘুরি করে। আসনটি বৃত্তের কেন্দ্র থেকে 1 মিটার (ব্যাসার্ধ)। যদি মেয়েটি 1.5 মিটার (রৈখিক স্থানচ্যুতি) একটি আর্ক ট্র্যাজেক্টোরিতে চলতে থাকে, তবে তার কৌণিক স্থানচ্যুতি কী?
- আপনার সমীকরণটি এইরকম হবে: = 1.5/1।
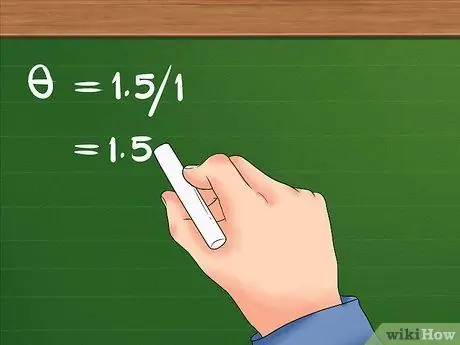
ধাপ 3. ব্যাসার্ধ দ্বারা রৈখিক স্থানচ্যুতি ভাগ করুন।
এই বিভাজনের ফলে বস্তুর কৌণিক স্থানচ্যুতি হবে।
- 1.5. 1.5 কে 1 দিয়ে ভাগ করার পর ফলাফল 1.5. 1.5। মেয়েটির কৌণিক স্থানচ্যুতি..। রেডিয়ান
- যেহেতু কৌণিক স্থানচ্যুতি পরিমাপ করে কোন বস্তু তার প্রাথমিক অবস্থান থেকে কতটা ঘুরছে, তাই এটি দূরত্ব নয়, একটি কোণ হিসাবে পরিমাপ করা উচিত। রেডিয়ান হল কোণ পরিমাপের জন্য ব্যবহৃত একক।
5 এর 5 ম অংশ: মাইগ্রেশন সম্পর্কে বোঝা
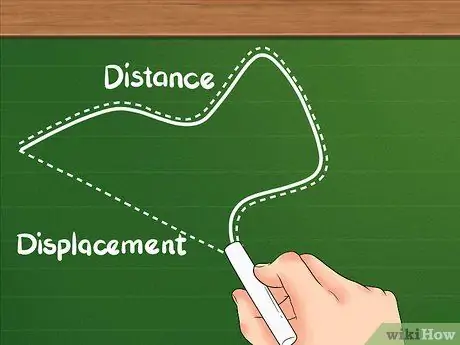
ধাপ 1. জানুন যে দূরত্বের স্থানচ্যুতি থেকে আলাদা সংজ্ঞা রয়েছে।
দূরত্ব দেখায় যে বস্তু দ্বারা মোট দূরত্ব কত দূর ভ্রমণ করেছে।
- দূরত্ব প্রায়ই একটি স্কেলার পরিমাণ হিসাবে পরিচিত হয়। দূরত্ব বস্তুর দিক নির্বিশেষে কোন বস্তু দ্বারা ভ্রমণ করা দূরত্ব দেখায়।
- উদাহরণস্বরূপ, যদি আপনি পূর্ব দিকে 2 ধাপ, 2 ধাপ দক্ষিণে, 2 ধাপ পশ্চিমে এবং তারপর 2 ধাপ উত্তরে হাঁটেন, তাহলে আপনি আপনার শুরুর অবস্থানে ফিরে আসবেন। যদিও আপনি মোটের মধ্যে দিয়ে গেছেন দূরত্ব 10 ধাপ দূরে, আপনি শুধু সরানো 0 ধাপ দূরে কারণ আপনার চূড়ান্ত অবস্থান আপনার শুরুর অবস্থানের সমান (আপনার পথ একটি বাক্সের অনুরূপ)।

ধাপ 2. বুঝুন যে স্থানচ্যুতি দুটি অবস্থানের মধ্যে পার্থক্য।
স্থানচ্যুতি দূরত্বের মত গতির মোট যোগফল নয়; শিফটগুলি আপনার শুরু এবং শেষ অবস্থানের মধ্যবর্তী এলাকায় ফোকাস করে।
- স্থানচ্যুতিকে ভেক্টর পরিমাণ বলা হয় এবং বস্তুর গতির দিক বিবেচনা করে বস্তুর অবস্থানের পরিবর্তন দেখায়।
- উদাহরণস্বরূপ, আপনি 5 ধাপের জন্য পূর্ব দিকে হাঁটুন। যদি আপনি পশ্চিমে 5 ধাপ পিছনে যান, তাহলে আপনি আপনার আসল অবস্থান থেকে বিপরীত দিকে চলে যাবেন। যদিও আপনি 10 টি ধাপ অতিক্রম করেছেন, আপনার অবস্থান পরিবর্তন হয়নি; আপনার স্থানচ্যুতি 0 ধাপ।

পদক্ষেপ 3. স্থানচ্যুতি কল্পনা করার চেষ্টা করার সময় সামনে এবং পিছনে শব্দগুলি মনে রাখবেন।
বিপরীত দিকে চললে বস্তুর স্থানচ্যুতি দূর হয়।
পিছনে পিছনে একটি ফুটবল কোচ কল্পনা করুন। খেলোয়াড়দের দিকে তিনি চিৎকার করার সাথে সাথে তিনি বেশ কয়েকবার বাম থেকে ডানে সরে গেলেন। যদি আপনি তাকে বাম থেকে ডানে সরে যেতে দেখেন, আপনি তার ভ্রমণের মোট দূরত্ব লক্ষ্য করেন। যাইহোক, ধরুন কোচ কোয়ার্টারব্যাকের সাথে কথা বলা বন্ধ করে দেয়। যদি সে স্থানান্তরিত হওয়ার আগে তার প্রাথমিক অবস্থানের চেয়ে ভিন্ন স্থানে থাকে, তাহলে আপনি প্রশিক্ষকের পদক্ষেপ পর্যবেক্ষণ করছেন।

ধাপ 4. জানুন যে স্থানচ্যুতি একটি সরল পথ ব্যবহার করে পরিমাপ করা হয়, বৃত্তাকার পথ নয়।
স্থানচ্যুতি খুঁজে পেতে, আপনাকে দুটি পয়েন্টের মধ্যে পার্থক্য গণনা করার জন্য সংক্ষিপ্ত এবং সবচেয়ে কার্যকর উপায় খুঁজে বের করতে হবে।
- একটি বৃত্তাকার পথ আপনাকে আপনার প্রারম্ভিক অবস্থান থেকে আপনার চূড়ান্ত অবস্থানে নিয়ে যাবে, কিন্তু এটি সবচেয়ে ছোট পথ নয়। আপনি এটি কল্পনা করতে সাহায্য করার জন্য, কল্পনা করুন যে আপনি একটি সরলরেখায় হাঁটছেন এবং আপনি একটি স্তম্ভ জুড়ে এসেছেন। আপনি এই স্তম্ভটি ভেঙে ফেলতে পারবেন না, তাই আপনি এটির চারপাশে যান। যদিও আপনার চূড়ান্ত অবস্থানটি যদি আপনি পিলারটি ভেঙে ফেলেন তবে সেই লক্ষ্যে পৌঁছানোর জন্য আপনাকে অতিরিক্ত পদক্ষেপের প্রয়োজন হবে।
- যদিও স্থানচ্যুতি একটি সরল পথের প্রতিনিধিত্ব করে, জেনে রাখুন যে আপনি একটি বস্তুর স্থানচ্যুতি পরিমাপ করতে পারেন বর্তমানে একটি বৃত্তাকার পথে সরানো। এই স্থানচ্যুতিকে কৌণিক স্থানচ্যুতি বলা হয় এবং প্রাথমিক অবস্থান থেকে চূড়ান্ত অবস্থানে সবচেয়ে ছোট পথ খুঁজে বের করে গণনা করা যায়।

ধাপ 5. জানুন যে স্থানচ্যুতি দূরত্বের বিপরীতে নেতিবাচক হতে পারে।
যদি আপনার প্রাথমিক দিকের বিপরীত দিকে অগ্রসর হয়ে আপনার চূড়ান্ত অবস্থানে পৌঁছানো হয়, তাহলে আপনার স্থানচ্যুতি নেতিবাচক।
- উদাহরণস্বরূপ, আমরা 5 ধাপ পূর্বে এবং তারপর 3 ধাপ পশ্চিমে হাঁটি। যদিও হিসাবের মাধ্যমে আপনি আপনার শুরুর অবস্থান থেকে 2 ধাপ সরে যান, আপনার স্থানচ্যুতি -2 কারণ আপনি বিপরীত দিকে এগিয়ে যাচ্ছেন। আপনার দূরত্ব সর্বদা ইতিবাচক হবে কারণ আপনি ধাপ, কিলোমিটার ইত্যাদিতে পিছনের দিকে গণনা করতে পারবেন না।
- নেতিবাচক স্থানচ্যুতি মানে এই নয় যে স্থানচ্যুতি হ্রাস পায়। নেতিবাচক মানে শুধু দিক বিপরীত।

ধাপ 6. উপলব্ধি করুন যে কখনও কখনও দূরত্ব এবং স্থানচ্যুতি একই হতে পারে।
যদি আপনি 25 টি ধাপে সোজা হেঁটে যান এবং থামেন, আপনি যে দূরত্বটি ভ্রমণ করবেন তা আপনার আসল অবস্থান থেকে স্থানান্তরের সমান হবে।
- এটি শুধুমাত্র তখনই প্রযোজ্য হয় যখন আপনি আপনার অবস্থান থেকে একটি সরলরেখায় একটি স্থান থেকে সরে যান। উদাহরণস্বরূপ, আপনি ক্যালিফোর্নিয়ার সান ফ্রান্সিসকোতে থাকেন এবং নেভাদার লাস ভেগাসে একটি নতুন চাকরি পান। আপনার কাজের কাছাকাছি হতে আপনাকে লাস ভেগাসে যেতে হবে। যদি আপনি একটি উড়োজাহাজে উঠেন যা উড়ে যায় সোজা সান ফ্রান্সিসকো থেকে লাস ভেগাস পর্যন্ত, আপনি একই দূরত্ব এবং স্থানচ্যুতি x ভ্রমণ করবেন।
- যাইহোক, যদি আপনি সান ফ্রান্সিসকো থেকে লাস ভেগাসে যান, আপনি x দূরত্ব ভ্রমণ করবেন, কিন্তু y দূরত্ব ভ্রমণ করবেন। যেহেতু গাড়ি চালানোর ক্ষেত্রে সাধারণত পরিবর্তনশীল দিক থাকে (এই রাস্তার পূর্ব দিকে, সেই রাস্তার পশ্চিমে), আপনি দুই শহরের মধ্যে সবচেয়ে কম দূরত্বের চেয়ে দীর্ঘ দূরত্ব ভ্রমণ করবেন।






