গতি গণনার W টি উপায়

2024 লেখক: Jason Gerald | [email protected]. সর্বশেষ পরিবর্তিত: 2024-01-16 19:13

গতি হল একটি সময়ে কত দ্রুত গতিতে একটি হিসাব। আপনি যদি কখনও চলন্ত গাড়ির স্পিডোমিটারের দিকে তাকিয়ে থাকেন তবে আপনি গতির গণনা দেখতে পাবেন - সুই যতদূর যাতায়াত করবে, গাড়ির গতি তত বেশি হবে। আপনার যে ধরনের তথ্য রয়েছে তার উপর নির্ভর করে গতি গণনা করার বিভিন্ন উপায় রয়েছে। সাধারণভাবে, সূত্র গতি = দূরত্ব/সময় (অথবা k = j/w) গতি গণনা করার সবচেয়ে সহজ উপায়।

ধাপ

পদ্ধতি 3 এর 1: স্ট্যান্ডার্ড স্পিড ক্যালকুলেশন ফর্মুলা ব্যবহার করা

ধাপ 1. একটি বস্তু কত দূরত্ব ভ্রমণ করেছে তা খুঁজুন।

যে মৌলিক সূত্রটি অধিকাংশ মানুষ কোন কিছুর গতি বের করতে ব্যবহার করে তা ব্যবহার করা খুবই সহজ। প্রথমত, আপনাকে জানতে হবে "পরিমাপ করা বস্তুটি কত দূরত্ব ভ্রমণ করেছে"। অন্য কথায়, বস্তুর প্রারম্ভিক বিন্দু এবং শেষ বিন্দুর মধ্যে দূরত্ব কত?

এই সূত্রটি একটি উদাহরণের মাধ্যমে বোঝা সহজ। ধরা যাক যে আমরা "161 কিলোমিটার" জন্য একটি খেলার মাঠে গাড়িতে ভ্রমণ করি। কয়েকটি ধাপে, আমরা সূত্রের গণনা সম্পন্ন করতে এই তথ্য ব্যবহার করতে পারি।

ধাপ ২. দূরত্বটি ভ্রমণ করতে বস্তুর যে সময় লাগে তা খুঁজুন।

আপনার পরবর্তী তথ্য প্রয়োজন একটি নির্দিষ্ট দূরত্বে পৌঁছাতে বস্তুর কতক্ষণ লাগে। অন্য কথায়, বস্তুটিকে শুরু বিন্দু থেকে শেষ বিন্দুতে যেতে কতক্ষণ সময় লাগে?

এই উদাহরণে, ধরা যাক বস্তুটি প্রায় লাগে। দুই ঘন্টা গন্তব্যে পৌঁছানোর জন্য।

ধাপ the. বস্তুর বেগ খুঁজে পেতে সময় নিয়ে দূরত্ব ভাগ করুন।

বস্তুর গতি জানতে আপনার কেবল এই দুটি টুকরো তথ্যের প্রয়োজন। সময়ের দূরত্ব বস্তুর বেগের সমান।

এই উদাহরণে, 161 কিলোমিটার/2 ঘন্টা = 80.5 কিলোমিটার/ঘন্টা.

ধাপ 4. ব্যবহৃত ইউনিট ভুলবেন না।

আপনার উত্তরে সঠিক ইউনিট ব্যবহার করা খুবই গুরুত্বপূর্ণ (যেমন প্রতি ঘন্টায় কিলোমিটার ইত্যাদি) এই ইউনিটগুলি ছাড়া, আপনার উত্তরের অর্থ বোঝা মানুষের পক্ষে খুব কঠিন। আপনি স্কুল থেকে অ্যাসাইনমেন্ট করার সময় ভুল ইউনিট ব্যবহার করলে পয়েন্টও হারাতে পারেন।

গতির একক হল সময়ের একক থেকে দূরত্বের একক । উদাহরণস্বরূপ, যেহেতু আমরা কিলোমিটারে দূরত্ব পরিমাপ করি এবং ঘন্টাগুলিতে সময়, তাই ব্যবহৃত ইউনিটগুলি কিলোমিটার/ঘন্টা (অথবা কিলোমিটার প্রতি ঘন্টা).

3 এর পদ্ধতি 2: আরও কঠিন গণনা সমাধান করা

ধাপ 1. দূরত্ব এবং সময়ের সমস্যা সমাধানের জন্য বিভিন্ন ভেরিয়েবল খুঁজুন।

একবার আপনি গতির মৌলিক সূত্রটি বুঝতে পারলে, আপনি এটি ব্যবহার করতে পারেন গতি ব্যতীত অন্যান্য গণনা করতে। উদাহরণস্বরূপ, যদি প্রথমে আপনি কেবল বস্তুর বেগ এবং অন্য একটি পরিবর্তনশীল জানেন, তাহলে আপনি অজানা তথ্য খুঁজে পেতে উপরের সূত্রটি পুনরায় সাজাতে পারেন।

• উদাহরণস্বরূপ, ধরা যাক যে আমরা জানি যে একটি ট্রেন চার ঘণ্টার জন্য 20 কিলোমিটার প্রতি ঘন্টায় ভ্রমণ করে, কিন্তু আমরা জানি না এটি কতদূর ভ্রমণ করেছে। খুঁজে বের করতে, আমরা নিম্নলিখিত পদ্ধতিতে সূত্রটি পুনর্বিন্যাস করতে পারি:

  গতি = দূরত্ব/সময়

  গতি × সময় = (দূরত্ব/সময়) × সময়

  গতি × সময় = দূরত্ব

  20 কিমি/ঘন্টা × 4 ঘন্টা = দূরত্ব = 80 কিলোমিটার

ধাপ 2. প্রয়োজন অনুযায়ী আপনি যে ইউনিটগুলি ব্যবহার করেন তা রূপান্তর করুন।

কখনও কখনও, আপনি একটি নির্দিষ্ট ইউনিট ব্যবহার করে গতি গণনা করতে পারেন, কিন্তু এটি অন্য ইউনিটে রূপান্তর করতে হবে। এই ক্ষেত্রে, সঠিক ইউনিট অনুযায়ী উত্তর পেতে আপনাকে একটি রূপান্তর ফ্যাক্টর ব্যবহার করতে হবে। এটি করার জন্য, কেবল ভগ্নাংশ আকারে ইউনিটগুলির মধ্যে সম্পর্ক লিখুন এবং গুণ করুন। গুণ করার সময়, অবাঞ্ছিত ইউনিট অপসারণের জন্য প্রয়োজন অনুযায়ী ভগ্নাংশকে বিপরীত করুন। এই পদ্ধতিটি শোনার চেয়ে অনেক সহজ!

• উদাহরণস্বরূপ, ধরা যাক যে উপরের উদাহরণ সমস্যাতে, আমাদের উত্তরটি কিলোমিটারের পরিবর্তে মাইলে প্রয়োজন। এক মাইল প্রায় 1.6 কিলোমিটার সমান। সুতরাং, আমরা রূপান্তরটি নিম্নরূপ করতে পারি:

  80 কিলোমিটার × 1 মাইল/1.6 কিলোমিটার = 50 মাইল

• মনে রাখবেন, কারণ ভগ্নাংশের নীচে কিলোমিটার দেখা যায়, এটি পূর্ববর্তী উত্তর থেকে কিলোমিটার সরিয়ে দেয়, তাই চূড়ান্ত ফলাফল মাইল ব্যবহার করে।
• এই ওয়েবসাইটটি সাধারণত ব্যবহৃত বেশিরভাগ ইউনিটের জন্য রূপান্তর বৈশিষ্ট্য সরবরাহ করে।

ধাপ 3. প্রয়োজন অনুসারে দূরত্ব সূত্রের সাথে "দূরত্ব" পরিবর্তনশীলটি প্রতিস্থাপন করুন।

বস্তু সবসময় সরল, মসৃণ পথে চলে না। যদি এটি সত্য হয়, তাহলে আপনি কেবলমাত্র একটি বেগের সূত্রের মধ্যে দূরত্বের একক হিসেবে একটি সংখ্যাসূচক মান লিখতে পারবেন না। যাইহোক, আপনাকে সূত্র k = j/w এ j অক্ষরটি একটি সূত্র দিয়ে প্রতিস্থাপন করতে হতে পারে যা বস্তুর দ্বারা ভ্রমণ করা দূরত্বের অনুরূপ।

• উদাহরণস্বরূপ, ধরা যাক যে একটি বিমান বাতাসের মধ্য দিয়ে 20 মাইল 5 বার দূরত্বে ঘুরছে। বিমানটি আধা ঘন্টার মধ্যে রাউন্ড সম্পন্ন করে। এই উদাহরণে, বিমানের গতি নির্ণয় করার আগে আমাদের এখনও সমগ্র ভ্রমণের মোট দূরত্ব খুঁজে বের করতে হবে। আমরা এই সূত্রে j এর পরিবর্তে একটি বৃত্তের চারপাশের দূরত্ব (এর চারপাশের দূরত্ব) গণনার জন্য সূত্রটি ব্যবহার করতে পারি। এই সূত্রটি পরিধি = 2πr যেখানে r = বৃত্তের ব্যাসার্ধ। এখানে এটি কিভাবে সমাধান করতে হয়:

  k = (2 × × r)/w

  k = (2 × × 10) /0.5

  k = 62.83/0.5 = 125.66 মাইল/ঘন্টা

ধাপ 4. বুঝুন যে k = j/w গড় বেগ দেয়।

বেগ খুঁজে পেতে আমরা যে সহজ এবং সহজ সূত্রটি ব্যবহার করি তার একটি ত্রুটি রয়েছে। ফলে মান টেকনিক্যালি গড় গতি। এর মানে হল যে সূত্রটি অনুমান করে যে আপনি যে বস্তুটি পরিমাপ করছেন তা একই গতি ব্যবহার করে যেমন এটি চলে। আমরা নিচে দেখব, এক মুহূর্তে কোনো বস্তুর বেগ খুঁজে পাওয়া অনেক কঠিন হবে।

এই পার্থক্য বোঝাতে, কল্পনা করুন যে আপনি শেষবার গাড়িতে ভ্রমণ করেছিলেন। এটা অসম্ভাব্য যে আপনি একই গতিতে ভ্রমণ করছেন যেমন আপনি ভ্রমণ করছেন। যাইহোক, আপনি সাধারণত স্বল্প গতিতে আপনার যাত্রা শুরু করবেন এবং ধীরে ধীরে আপনার গতি বাড়াবেন, লাল বাতি, ট্রাফিক জ্যাম ইত্যাদির কারণে থেমে যাবেন। আপনি যদি ভ্রমণের সময় গতি খোঁজার জন্য স্ট্যান্ডার্ড স্পিড ফর্মুলা ব্যবহার করেন, তাহলে সেই গতির পরিবর্তনগুলি সনাক্ত করা যাবে না। যাইহোক, আপনি একটি উত্তর পাবেন যা আপনার ভ্রমণের সমস্ত গতির পার্থক্যের গড় গতি দেখায়।

3 এর পদ্ধতি 3: তাত্ক্ষণিক গতি গণনা করা

বিঃদ্রঃ:

এই বিভাগটি এমন কৌশলগুলি ব্যবহার করে যা এমন লোকদের কাছে কম পরিচিত যারা কখনও ক্যালকুলাস অধ্যয়ন করেননি। সাহায্যের জন্য ক্যালকুলাসে আমাদের নিবন্ধগুলি পড়ুন।

ধাপ 1. বুঝুন যে বেগকে ত্বরণের হার হিসাবে সংজ্ঞায়িত করা হয়।

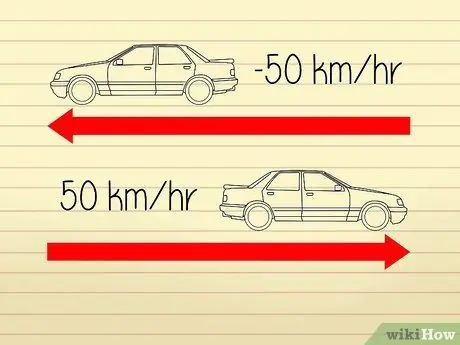
উচ্চ-স্তরের বেগ গণনা বেশ বিভ্রান্তিকর কারণ গণিতবিদ এবং বিজ্ঞানীরা "গতি" এবং "ত্বরণ" বর্ণনা করার জন্য বিভিন্ন সংজ্ঞা ব্যবহার করেন। ত্বরণের দুটি উপাদান রয়েছে: একটি "হার" এবং একটি "দিক"। হার বস্তুর গতির সমান। দিক পরিবর্তনের ফলে ত্বরণে পরিবর্তন হবে, কিন্তু বেগের পরিবর্তন হবে না।

• উদাহরণস্বরূপ, ধরা যাক যে দুটি গাড়ি বিপরীত দিকে যাচ্ছে। উভয় গাড়ির স্পিডোমিটারগুলি 50 কিমি/ঘন্টা চিত্র প্রদর্শন করে যাতে তারা উভয়ই একই গতিতে ভ্রমণ করে। যাইহোক, যেহেতু গাড়িগুলি একে অপরের থেকে দূরে সরে যাচ্ছে, আমরা বলতে পারি যে একটি গাড়ির -50 কিমি/ঘন্টা "ত্বরণ" এবং অন্যটির 50 কিলোমিটার/ঘন্টা "ত্বরণ" রয়েছে।
• তাত্ক্ষণিক বেগ গণনার মতো, আপনি তাত্ক্ষণিক ত্বরণ গণনাও করতে পারেন।

ধাপ 2. নেতিবাচক ত্বরণ পরিমাপ করতে পরম মান ব্যবহার করুন।

একটি বস্তুর ত্বরণের negativeণাত্মক হার থাকতে পারে (যদি এটি অন্য বস্তুর সাপেক্ষে negativeণাত্মক দিকে অগ্রসর হয়)। যাইহোক, কোন নেতিবাচক গতি নেই। সুতরাং, এই ক্ষেত্রে, হারের পরম মান বস্তুর বেগ নির্দেশ করে।

এই কারণে, উপরের উদাহরণ সমস্যা, উভয় গাড়ির একটি গতি আছে 50 কিমি/ঘন্টা.

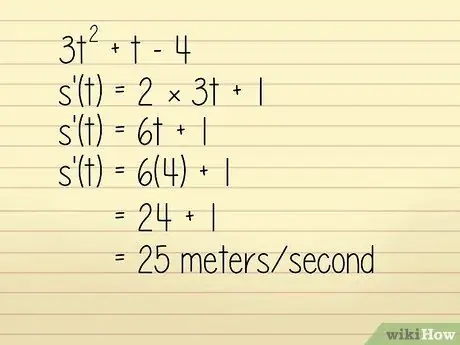
পদক্ষেপ 3. ফাংশনের অবস্থানের ডেরিভেটিভ নিন।

যদি আপনার একটি ফাংশন k (w) থাকে যা সময় গণনা করার প্রয়োজন ছাড়াই একটি বস্তুর অবস্থান দেখায়, k (w) এর ডেরিভেটিভ সময় ছাড়াই ত্বরণ দেখাবে। শুধু এই ফর্মুলায় সময়ের মান প্লাগ করুন যাতে পরিবর্তনশীল w (বা যাই হোক না কেন সময় মান ব্যবহার করা হয়) সেই সময় অনুযায়ী ত্বরান্বিত হয়। এখান থেকে, আপনি সহজেই বস্তুর বেগ খুঁজে পেতে পারেন।

• উদাহরণস্বরূপ, ধরা যাক যে এক মিটারে একটি বস্তুর অবস্থান 3q সমীকরণে বর্ণিত হয়েছে² + w - 4 যেখানে w = সেকেন্ডে সময়। আমরা বস্তুর বেগ w = 4 সেকেন্ডে জানতে চাই। এই ক্ষেত্রে, আপনি এটি দ্বারা সমাধান করতে পারেন:

  3w² +w - 4

  k '(w) = 2 × 3w + 1

  k '(w) = 6w + 1

• এখন, আমরা w = 4 লিখি:

  k '(w) = 6 (4) + 1 = 24 + 1 = 25 মিটার/সেকেন্ড । টেকনিক্যালি এটি ত্বরণের একটি হিসাব, কিন্তু যেহেতু এটি ইতিবাচক এবং প্রশ্নে দিকনির্দেশ উল্লেখ করা হয়নি, তাই আমরা বেগ ব্যবহার করতে এটি ব্যবহার করতে পারি।

ধাপ 4. অবিচ্ছেদ্য ত্বরণ ফাংশন নিন।

অ্যাক্সিলারেশন হল সময়ের সাথে একটি বস্তুর ত্বরণের পরিবর্তন পরিমাপ করার একটি উপায়। এই নিবন্ধটি সম্পূর্ণরূপে ব্যাখ্যা করার জন্য এই বিষয়টি খুব জটিল। যাইহোক, এটি লক্ষ্য করা দরকার যে যখন আপনার একটি ফাংশন a (w) থাকে যা সময়ের সাথে সাথে ত্বরণকে প্রতিনিধিত্ব করে, a (w) এর অবিচ্ছেদ্য সেই সময়ের উপর ভিত্তি করে ত্বরণের ফলাফল ফিরিয়ে দেবে। মনে রাখবেন, একটি বস্তুর প্রাথমিক ত্বরণ জানা খুবই উপকারী যাতে আপনি একটি অসীম অবিচ্ছেদ্য থেকে সেই ফলাফলের ধ্রুবক সংজ্ঞায়িত করতে পারেন।

• উদাহরণস্বরূপ, ধরা যাক যে একটি বস্তুর একটি ধ্রুবক ত্বরণ আছে (m/s তে² a (w) = -30 এর ফলে। এছাড়াও বলুন যে বস্তুর 10 m/s এর প্রাথমিক ত্বরণ রয়েছে। আমাদের গতি বের করতে হবে w = 12 সেকেন্ডে। এই ক্ষেত্রে, আমরা এর দ্বারা সমাধান করতে পারি:

  a (w) = -30

  p (w) = a (w) dw = -30dw = -30w + c

• C খুঁজে পেতে, আমরা w = 0. এর জন্য p (w) সমাধান করব। মনে রাখবেন বস্তুর প্রাথমিক ত্বরণ 10 m/s।

  p (0) = 10 = -30 (0) + C

  10 = C, তাই p (w) = -30w + 10

• এখন, আমরা w = 12 সেকেন্ড প্রবেশ করতে পারি।

  p (12) = -30 (12) + 10 = -360 + 10 = -350। যেহেতু বেগ হল ত্বরণের একটি পরম মান, তাই বস্তুর বেগ হল 350 মিটার/সেকেন্ড.

পরামর্শ

• অনুশীলন দুর্দান্ত করে তোলে! উপরের উদাহরণ সমস্যার মধ্যে সংখ্যাগুলি প্রতিস্থাপন করে আপনার নিজের প্রশ্ন তৈরি করার চেষ্টা করুন।
• যদি আপনি দ্রুত গণনার গতির জন্য ক্যালকুলাস অনুশীলনের একটি দ্রুত উপায় খুঁজছেন, এখানে অনলাইন ডেরিভেটিভ ক্যালকুলেটর এবং এখানে অনলাইন অবিচ্ছেদ্য ক্যালকুলেটর ব্যবহার করুন।