কিভাবে গড় গতি গণনা করবেন: 12 টি ধাপ (ছবি সহ)

2024 লেখক: Jason Gerald | [email protected]. সর্বশেষ পরিবর্তিত: 2024-02-01 14:11

গড় গতি গণনা করার জন্য আপনাকে যা করতে হবে তা হল মোট স্থানচ্যুতি। অথবা অবস্থান পরিবর্তন, এবং মোট সময়। মনে রাখবেন যে বেগ একটি বস্তুর দিক এবং গতিও গণনা করে, তাই আপনার উত্তরে একটি দিক অন্তর্ভুক্ত করুন, যেমন "উত্তর," "সামনে," বা "বাম।" যদি আপনার গতির হিসাবের সমস্যাটিও ধ্রুবক ত্বরণকে অন্তর্ভুক্ত করে, আপনি উত্তরটি আরও সহজভাবে খুঁজে পেতে দ্রুত উপায় শিখতে পারেন।

ধাপ

2 এর পদ্ধতি 1: স্থানচ্যুতি এবং সময়ের গড় বেগ গণনা করা

ধাপ 1. মনে রাখবেন যে বেগ একটি বস্তুর গতি এবং দিক উভয়ই অন্তর্ভুক্ত করে।

বেগ একটি বস্তুর অবস্থান পরিবর্তনের হার বর্ণনা করে। এটি কেবল বস্তুটি কত দ্রুত গতিতে চলেছে তা নয়, বরং এর দিকনির্দেশনাও। "100 মিটার প্রতি সেকেন্ড দক্ষিণমুখী" একটি পূর্ব গতির মান "100 মিটার প্রতি সেকেন্ড পূর্ব দিকে" এর চেয়ে আলাদা।

• যে পরিমাণে দিক আছে তাকে ভেক্টর কোয়ান্টিটি বলা হয়। ভেরিয়েবলের উপরে একটি তীর লিখে এই পরিমাণটিকে একটি দিকনির্দেশহীন পরিমাণ থেকে আলাদা করা যায় যাকে স্কেলার পরিমাণ বলা হয়। উদাহরণস্বরূপ, স্বরলিপি v হারের প্রতিনিধিত্ব করে, যখন স্বরলিপি v ^→ গতি বা গতি + দিক নির্দেশ করে। এই নিবন্ধে ব্যবহৃত v স্বরলিপি গতির প্রতিনিধিত্ব করে।
• বৈজ্ঞানিক সমস্যাগুলিতে, আপনার দূরত্ব প্রকাশের জন্য মিটার বা অন্যান্য মেট্রিক ইউনিট ব্যবহার করা উচিত, যখন দৈনন্দিন কাজে আপনি যে কোন ইউনিট ব্যবহার করতে পারেন।

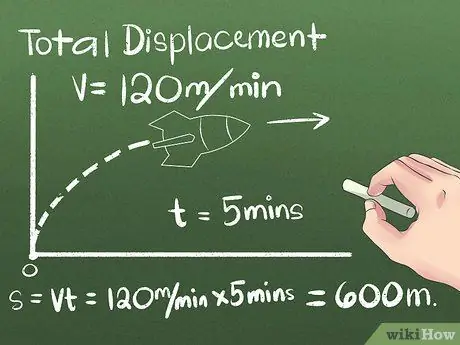
ধাপ 2. মোট স্থানচ্যুতি মান খুঁজুন।

স্থানচ্যুতি হচ্ছে বস্তুর অবস্থানের পরিবর্তন, অথবা তার শুরু এবং শেষ বিন্দুর মধ্যে দূরত্ব এবং দিক। বস্তুটি তার চূড়ান্ত অবস্থানে পৌঁছানোর আগে যে দিকে চলে তা উপেক্ষা করা যেতে পারে, কারণ শুধুমাত্র শুরু এবং শেষ পয়েন্টের মধ্যে দূরত্ব বিবেচনায় নেওয়া হয়। প্রথম উদাহরণের জন্য, আমরা একটি বস্তু ব্যবহার করব যা একটি গতিতে একটি ধ্রুব গতিতে চলবে:

• বলুন একটি রকেট প্রতি মিনিটে 120 মিটার ধ্রুব গতিতে 5 মিনিটের জন্য উত্তর দিকে অগ্রসর হচ্ছে। চূড়ান্ত অবস্থান গণনা করার জন্য, সূত্রটি ব্যবহার করুন = vt, অথবা ব্যবহারিক চিন্তাভাবনা ব্যবহার করে রকেটে ভ্রমণের দূরত্ব গণনা করুন (5 মিনিট) (120 মিটার/মিনিট) = 600 মিটার উত্তরে শুরু বিন্দু থেকে।
• ধ্রুব ত্বরণ জড়িত সমস্যার জন্য, আপনি s = vt + at দিয়ে তাদের সমাধান করতে পারেন², অথবা উত্তর খুঁজতে অন্য অংশে বর্ণিত সংক্ষিপ্ত পদ্ধতিটি ব্যবহার করুন।

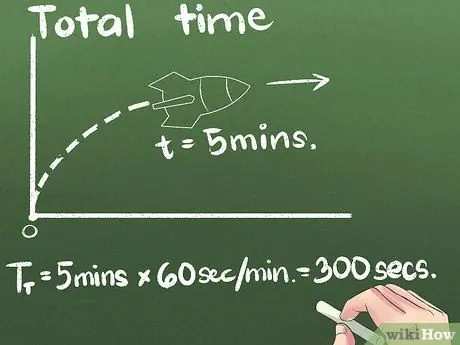
ধাপ 3. মোট ব্যয় করা সময় খুঁজুন।

আমাদের উদাহরণে, রকেটটি 5 মিনিটের জন্য এগিয়ে চলেছে। আপনি সময়ের যেকোনো ইউনিটে গড় গতি প্রকাশ করতে পারেন, কিন্তু দ্বিতীয়টি আন্তর্জাতিক বৈজ্ঞানিক মান ইউনিট। আমরা এই উদাহরণে সেকেন্ডের একক পরিবর্তন করব: (5 মিনিট) x (60 সেকেন্ড/মিনিট) = 300 সেকেন্ড.

এমনকি বৈজ্ঞানিক সমস্যাগুলিতেও, যদি প্রশ্নটি ঘন্টা বা সময়ের একটি বড় ইউনিট ব্যবহার করে, তাহলে প্রথমে গতি গণনা করা সহজ হবে, তারপর চূড়ান্ত উত্তরটিকে মিটার/সেকেন্ডে রূপান্তর করুন।

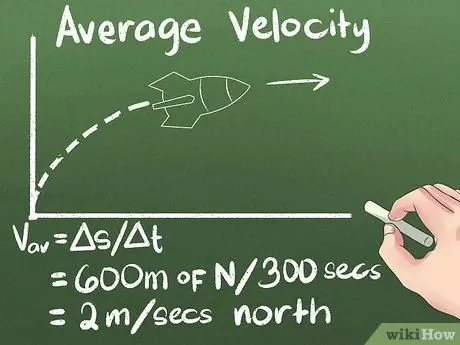
পদক্ষেপ 4. সময়ের সাথে স্থানচ্যুতি হিসাবে গড় বেগ গণনা করুন।

যদি আপনি জানেন যে কোন বস্তু কতদূর অগ্রসর হচ্ছে, এবং সেখানে পৌঁছাতে কত সময় লাগবে, তাহলে আপনি জানতে পারবেন যে এটি কত দ্রুত এগিয়ে যাচ্ছে। সুতরাং আমরা যে উদাহরণটি ব্যবহার করছি, রকেটের গড় গতি (600 মিটার উত্তর) / (300 সেকেন্ড) = 2 মিটার/সেকেন্ড উত্তর.

• একটি দিক অন্তর্ভুক্ত করতে মনে রাখবেন (যেমন "সামনে" বা "উত্তর")।
• সূত্রে v_av = s/Δt । বদ্বীপ প্রতীকটির অর্থ "পরিবর্তন", তাই s/Δt এর অর্থ "সময়ের সাথে অবস্থানের পরিবর্তন।"
• গড় গতি v হিসাবে লেখা যেতে পারে_av, অথবা এর উপরে একটি অনুভূমিক রেখা সহ একটি v হিসাবে।

ধাপ 5. আরো জটিল সমস্যার সমাধান করুন।

যদি কোন বস্তু তার দিক বা গতি পরিবর্তন করে, তাহলে বিভ্রান্ত হবেন না। গড় গতি এখনও মোট স্থানচ্যুতি এবং মোট সময় থেকে "শুধুমাত্র" গণনা করা হয়। শুরু এবং শেষ পয়েন্টের মধ্যে যা ঘটে তা আপনি উপেক্ষা করতে পারেন। নীচে একটি বস্তুর কয়েকটি স্থানান্তর এবং মোট সময় নিয়ে ভ্রমণের কিছু উদাহরণ রয়েছে, এবং এইভাবে, একই গড় বেগ:

• আনা 1 সেকেন্ডের জন্য 1 মিটার/সেকেন্ডে পশ্চিমে হাঁটেন, তারপর হঠাৎ 3 মিটার/সেকেন্ডে ত্বরান্বিত হয় এবং 2 সেকেন্ডের জন্য পশ্চিমে হাঁটতে থাকে। মোট স্থানচ্যুতি হল (1 মি/সেকেন্ড পশ্চিম দিকে) (2 সেকেন্ড) + (3 মি/সেকেন্ড পশ্চিম দিকে) (2 সেকেন্ড) = 8 মিটার পশ্চিম দিকে। মোট সময় 2 সেকেন্ড + 2 সেকেন্ড = 4 সেকেন্ড। সুতরাং গড় গতি 8 মিটার পশ্চিমে/ 4 সেকেন্ড = 2 মিটার/দ্বিতীয় পশ্চিমে।

• বার্ট 5 সেকেন্ডের জন্য 5 মিটার/সেকেন্ডে পশ্চিমে হাঁটেন, তারপর ঘুরে দাঁড়ান এবং 1 সেকেন্ডের জন্য 7 মিটার/সেকেন্ডে পূর্ব দিকে হাঁটেন। আমরা পূর্বমুখী আন্দোলনকে "negativeণাত্মক পশ্চিমমুখী গতি" হিসেবে ভাবতে পারি তাই মোট স্থানচ্যুতি = (5 মিটার/সেকেন্ড পশ্চিম দিকে) (3 সেকেন্ড) + (-7 মি/সেকেন্ড পশ্চিম দিকে) (1 সেকেন্ড) = 8 মিটার। মোট সময় = 4 সেকেন্ড। গড় গতি = 8 মিটার পশ্চিমে / 4 সেকেন্ড = 2 মিটার/দ্বিতীয় পশ্চিমে।

• শার্লট উত্তর 1 মিটার হাঁটলেন এবং তারপর পশ্চিম 8 মিটার, তারপর দক্ষিণ 1 মিটার হাঁটলেন। পুরো যাত্রা শেষ করতে সময় লাগে 4 সেকেন্ড। কাগজের একটি টুকরোতে ডায়াগ্রামটি আঁকুন, এবং আপনি দেখতে পাবেন শেষ বিন্দুটি শুরুর স্থান থেকে 8 মিটার পশ্চিমে, তাই এই মানটি স্থানচ্যুতি। মোট সময় লাগে 4 সেকেন্ড, তাই গড় গতি 8 মিটার পশ্চিমে / 4 সেকেন্ড = 2 মিটার/দ্বিতীয় পশ্চিমে।

  2 এর পদ্ধতি 2: স্থির ত্বরণ গড় বেগ গণনা

  

  ধাপ 1. প্রাথমিক বেগ এবং ধ্রুব ত্বরণ বিবেচনা করুন।

  ধরা যাক আমাদের সমস্যা হল "একটি সাইকেল ডান দিকে 5 মি/সেকেন্ডের গতিতে চলেছে, 2 মি/সেকেন্ডের ধ্রুব ত্বরণ সহ²। যদি এই সাইকেলটি 5 সেকেন্ডের জন্য চলাচল করে, তাহলে এর গড় গতি কত?"

  যদি ইউনিট "মিটার/সেকেন্ড²"আপনাকে বিভ্রান্ত করার জন্য, এটি" মিটার/সেকেন্ড/সেকেন্ড "বা" মিটার প্রতি সেকেন্ড প্রতি সেকেন্ডে লিখুন। "2 মিটার/সেকেন্ড/সেকেন্ডের একটি ত্বরণ মানে গতি প্রতি সেকেন্ডে 2 মিটার প্রতি সেকেন্ড বাড়ছে।

  

  পদক্ষেপ 2. চূড়ান্ত বেগ খুঁজে পেতে ত্বরণ ব্যবহার করুন।

  স্বরলিপি দ্বারা চিহ্নিত করা ত্বরণ, বেগের হার (বা হার)। গতি বৃদ্ধি একটি ধ্রুবক হারে বৃদ্ধি পায়। আপনি সাইকেল ভ্রমণের সময় বিভিন্ন সময়ে গতি খুঁজে পেতে ত্বরণ ব্যবহার করে একটি ছক আঁকতে পারেন। সমস্যাটির শেষ বিন্দু (t = 5 সেকেন্ডে) খুঁজে পেতে আমাদের এই টেবিলটি তৈরি করতে হবে, কিন্তু আপনার জন্য এই ধারণাটি উপলব্ধি করা সহজ করার জন্য আমরা একটি দীর্ঘ টেবিল তৈরি করব:

  • প্রারম্ভিক সময়ে (সময় t = 0 সেকেন্ড), সাইকেলটি 5 মিটার/সেকেন্ড গতিতে এগিয়ে চলেছে।
  • 1 সেকেন্ডের পর (t = 1), সাইকেল 5 মিটার/সেকেন্ডের গতিতে = 5 মিটার/সেকেন্ডে²) (1 সেকেন্ড) = 7 মিটার/সেকেন্ড।
  • T = 2 এ, সাইকেল 5+ (2) (2) = 9 মিটার/সেকেন্ডের গতিতে ডানদিকে চলে যাচ্ছে।
  • T = 3 এ, সাইকেল 5+ (2) (3) = 11 মিটার/সেকেন্ডের গতিতে ডানদিকে চলে যাচ্ছে।
  • T = 4 এ, সাইকেল ডানদিকে 5+ (2) (4) = 13 মিটার/সেকেন্ড গতিতে চলে যাচ্ছে।
  • T = 5 এ, সাইকেলটি 5+ (2) (5) = গতিতে ডানদিকে চলে যাচ্ছে 15 মিটার/সেকেন্ড.

  

  পদক্ষেপ 3. গড় গতি খুঁজে পেতে এই সূত্রটি ব্যবহার করুন।

  যদি এবং "শুধুমাত্র" যদি ত্বরণ ধ্রুব থাকে, গড় বেগ চূড়ান্ত এবং প্রাথমিক বেগের সমষ্টির গড় মানের সমান হবে। (ভি_চ +v_আমি)/2 । উপরের উদাহরণের সমস্যার জন্য, সাইকেলের প্রাথমিক গতি হল v_আমি 5 মিটার/সেকেন্ড আমরা হিসাব করার পর, চূড়ান্ত বেগ হল v_চ 15 মিটার/সেকেন্ড এই দুটি মান একসাথে যোগ করলে, আমরা (15 মিটার/সেকেন্ড + 5 মিটার/সেকেন্ড)/2 = (20 মিটার/সেকেন্ড)/2 = পাই 10 মিটার/সেকেন্ড ডান দিক.

  • দিকটি অন্তর্ভুক্ত করতে ভুলবেন না, এই ক্ষেত্রে "ঠিক"।
  • এই পদটি v হিসাবে লেখা যেতে পারে₀ (সময় 0, বা প্রাথমিক বেগ) এবং v (চূড়ান্ত বেগ)।

  

  ধাপ 4. স্বজ্ঞাতভাবে গড় বেগ সূত্র বুঝুন।

  গড় বেগ বের করার জন্য, আমরা যে কোন সময়ে বেগ ব্যবহার করতে পারি এবং তাদের সকলের জন্য গড় খুঁজে পেতে পারি। (এটি একটি গড়ের সংজ্ঞা।) যেহেতু এর জন্য ক্যালকুলাস বা অসীম সময় প্রয়োজন, তাই এই সূত্রটি আরও স্বজ্ঞাতভাবে বুঝুন। প্রতিটি সময় নেওয়ার পরিবর্তে, দুটি টাইম পয়েন্টের গড় বেগ গণনা করুন এবং ফলাফল দেখুন। সময়ের মধ্যে একটি বিন্দু রাইড শুরুর কাছাকাছি, যেখানে বাইকটি ধীরে ধীরে চলছে, এবং অন্য একটি বিন্দু শেষ বিন্দুর কাছাকাছি যেখানে বাইকটি দ্রুত গতিতে যাচ্ছে।

  

  ধাপ 5. স্বজ্ঞাত তত্ত্ব পরীক্ষা করুন।

  সময় বিভিন্ন পয়েন্টে বেগ নির্ধারণ করতে উপরের টেবিল ব্যবহার করুন। আমাদের মানদণ্ড পূরণ করে এমন কিছু জোড়া হল (t = 0, t = 5), (t = 1, t = 4), অথবা (t = 2, t = 3)। আপনি চাইলে এই ফর্মুলা টি পূর্ণসংখ্যা ছাড়াও টি মান দিয়ে পরীক্ষা করতে পারেন।

  আপনি যে কোন পয়েন্টের চয়ন করুন, সেই সময়ে গড় বেগ সর্বদা একই থাকবে। উদাহরণস্বরূপ, ((5+15)/2), ((7+13)/2), অথবা ((9+11)/2) ডানদিকে সব 10 মিটার/সেকেন্ড সমান।

  

  পদক্ষেপ 6. স্বজ্ঞাত ব্যাখ্যা সম্পূর্ণ করুন।

  যদি আমরা এই পদ্ধতিটি প্রতিবার নেওয়া তালিকার সাথে ব্যবহার করি, তাহলে আমরা ট্রিপের প্রথমার্ধ এবং ট্রিপের দ্বিতীয়ার্ধের গড় হিসাব করতে থাকব। প্রতিটি অর্ধেক কভার করতে সময় লাগে একই, তাই আমরা গণনা শেষ করার সময় কোন গতি হারিয়ে যায় না।

  • যেহেতু উভয় জোড়া একই ফলাফল দেবে, তাই এই গতির গড়ও একই মানের হবে। আমাদের উদাহরণে, পুরোটির গতি "10 মিটার/সেকেন্ড ডানদিকে" এখনও 10 মিটার/সেকেন্ড ডানদিকে থাকবে।
  • আমরা যেকোনো জোড়ার গড় হিসাব করে এই মানটি খুঁজে পেতে পারি, উদাহরণস্বরূপ প্রাথমিক এবং চূড়ান্ত বেগ। আমাদের উদাহরণে, এই গতিগুলি টি = 0 এবং টি = 5 এ পৌঁছেছে এবং উপরের সূত্রটি ব্যবহার করে গণনা করা যেতে পারে: (5+15)/2 = 10 মিটার/সেকেন্ড ডানদিকে।

  

  ধাপ 7. গাণিতিকভাবে এই সূত্রটি বুঝুন।

  যদি আপনি সূত্র হিসাবে লিখিত প্রমাণের সাথে আরও আরামদায়ক হন, তাহলে আপনি একটি সূত্র দিয়ে শুরু করতে পারেন যা ধ্রুব ত্বরণ ধরে নিয়ে ভ্রমণের দূরত্ব গণনা করতে পারে এবং সেখান থেকে সূত্রটি বের করতে পারে:

  • s = v_আমিt + এ²। (টেকনিক্যালি s এবং t, অথবা অবস্থানের পরিবর্তন এবং সময়ের সাথে পরিবর্তন, কিন্তু আপনি s এবং t লিখে থাকলে আপনিও বুঝতে পারবেন।)
  • গড় গতি v_av s/t হিসাবে সংজ্ঞায়িত, তাই s/t আকারে সূত্রটি লিখুন।
  • v_av = s/t = v_আমি + এ
  • ত্বরণ x সময় মোট বেগের পরিবর্তনের সমান, অথবা v_চ - ভি_আমি। সুতরাং আমরা সূত্রে "এ" প্রতিস্থাপন করতে পারি, এবং পেতে পারি:
  • v_av = v_আমি + (ভি_চ - ভি_আমি).
  • সরলীকরণ: v_av = v_আমি + v_চ - ভি_আমি = v_আমি + v_চ = (ভি_চ +v_আমি)/2.

  পরামর্শ

  • বেগ গতি থেকে আলাদা কারণ বেগ একটি ভেক্টর পরিমাণ যেখানে গতি একটি স্কেলার পরিমাণ। ভেক্টর পরিমাণে দিক এবং মাত্রা উভয়ই জড়িত, যখন স্কেলার পরিমাণ শুধুমাত্র মাত্রা জড়িত।
  • যদি বস্তুটি এক মাত্রায় চলে, যেমন বাম-ডান, আপনি একটি দিক নির্দেশ করতে একটি ধনাত্মক সংখ্যা ব্যবহার করতে পারেন (যেমন ডান) এবং একটি negativeণাত্মক সংখ্যা অন্য দিক নির্দেশ করতে (বাম)। আপনার পৃষ্ঠার শীর্ষে এই স্বরলিপি লিখুন যাতে এটি আপনার কাজ পড়া লোকদের কাছে স্পষ্ট হয়।