বিভাগ করার 5 টি উপায়

2024 লেখক: Jason Gerald | [email protected]. সর্বশেষ পরিবর্তিত: 2024-01-15 08:10

বিভাজন করার বিভিন্ন উপায় রয়েছে। আপনি দশমিক, ভগ্নাংশ বা এমনকি সূচকগুলি ভাগ করতে পারেন এবং দীর্ঘ বা সংক্ষিপ্ত বিভাগ ব্যবহার করতে পারেন। আপনি যদি সংখ্যা বিভাজনের বিভিন্ন উপায় জানতে চান, তাহলে নিচের ধাপগুলো অনুসরণ করুন।

ধাপ

পদ্ধতি 1 এর 5: দীর্ঘ সিরিজ বিভাগ সম্পাদন

ধাপ 1. প্রশ্নগুলো লিখ।

দীর্ঘ বিভাজন করার জন্য, বিভাজক বারের বাইরে হর (যে সংখ্যাটি বিভাজিত হবে) এবং বিভাজক বারের ভিতরে সংখ্যার (বিভক্ত হওয়ার সংখ্যা) রাখুন।

উদাহরণস্বরূপ: 136 3

ধাপ ২। সংখ্যার প্রথম অঙ্ককে হর দ্বারা ভাগ করুন (যদি সম্ভব হয়)।

এই উদাহরণে, 1 3 দ্বারা বিভাজ্য নয় তাই ভাজক বারের উপরে 0 রাখুন এবং পরবর্তী ধাপে যান। 0 দ্বারা 1 বিয়োগ করুন এবং ফলাফলটি 1 নম্বরের অধীনে রাখুন।

ধাপ the. সংখ্যার প্রথম অঙ্কের অবশিষ্টাংশের সংখ্যা এবং হর দ্বারা সংখ্যার দ্বিতীয় সংখ্যা ভাগ করুন।

যেহেতু 1 কে 3 দ্বারা ভাগ করা যায় না, তাই 1 নম্বরটি এখনও ব্যবহৃত হয়। আপনাকে 3 বিয়োগ করতে হবে। এখন, 13 দ্বারা 3 ভাগ করুন। যেহেতু 3 x 4 = 12, 4 কে বিভাজক বারের উপরে (0 এর ডানদিকে) রাখুন, তারপর 13 দ্বারা 12 বিয়োগ করুন এবং এর নীচে ফলাফল লিখুন।

ধাপ 4. অবশিষ্ট সংখ্যাগুলি হর দ্বারা ভাগ করুন।

16 পেতে 1 এর ডানদিকে 6 নম্বরটি কম করুন। এখন, 16 দ্বারা 3 ভাগ করুন। যেহেতু 3 x 5 = 15, 4 নম্বরটির ডানদিকে 5 নম্বরটি লিখুন এবং 15 দ্বারা 16 বিয়োগ করুন এবং ফলাফল লিখুন (16-15 = 1) এর নিচে।

ধাপ ৫। ভাগের পাশে বাকীটা লিখ।

আপনার চূড়ান্ত উত্তর 45 টি বাকি আছে, অথবা 45 R1।

5 এর পদ্ধতি 2: সংক্ষিপ্ত বিভাগগুলি সম্পাদন করা

ধাপ 1. প্রশ্নগুলো লিখ।

বিভাজক বারের বাইরে হর (ভাগ করার সংখ্যা), এবং বিভাজক বারের ভিতরে সংখ্যার (ভাগ করার সংখ্যা) লিখুন। উল্লেখ্য, সংক্ষিপ্ত বিভাজনে, হর এক অঙ্কের বেশি হতে পারে না।

উদাহরণস্বরূপ, 518 4

ধাপ 2. হর দ্বারা সংখ্যার প্রথম অঙ্ক ভাগ করুন।

5 4 = 1 আর 1। লম্বা বিভাজক বারের উপরে ভাগফল (1) রাখুন। সংখ্যার প্রথম অঙ্কের উপরে অবশিষ্টাংশ লিখুন। 5 থেকে 4 ভাগ করার সময় আপনার 1 টি বাকি আছে তা মনে করিয়ে দেওয়ার জন্য 5 এর উপরে একটি ছোট 1 রাখুন। 518 এখন এইরকম হওয়া উচিত: 5¹18

ধাপ the. অবশিষ্ট থেকে গঠিত সংখ্যা এবং সংখ্যার দ্বিতীয় অঙ্ককে হর দ্বারা ভাগ করুন।

পরবর্তী সংখ্যা হল 11 যা অবশিষ্ট মান (1) এবং সংখ্যার দ্বিতীয় সংখ্যা (1) থেকে প্রাপ্ত। 11 4 = 2 R 3 কারণ 4 x 2 = 8 অবশিষ্ট 3 দিয়ে। 3 ওভার 1 রাখুন। প্রাথমিক অংক (518) এখন এইরকম দেখাচ্ছে: 5¹1³8

ধাপ 4. অবশিষ্ট সংখ্যাকে হর দ্বারা ভাগ করুন।

অবশিষ্ট সংখ্যা 38; সংখ্যাটি পূর্ববর্তী পর্যায়ের অবশিষ্টাংশ থেকে আসে এবং 8 হল সংখ্যার শেষ সংখ্যা। 38 4 = 9 R2 গণনা করুন। যেহেতু 4 x 9 = 36, বিভাগ বারের উপরে "R2" লিখুন কারণ 38 - 36 = 2।

ধাপ 5. চূড়ান্ত উত্তর লিখুন।

চূড়ান্ত ফলাফল এবং ভাগফল বিভাজক বারের উপরে। উত্তর 518 4 = 129 R2।

5 এর 3 পদ্ধতি: ভগ্নাংশ ভাগ করুন

ধাপ 1. প্রশ্নগুলো লিখ।

একটি ভগ্নাংশ ভাগ করার জন্য, কেবল প্রথম ভগ্নাংশটি লিখুন তারপর ভাগ চিহ্ন এবং তারপর দ্বিতীয় ভগ্নাংশ।

উদাহরণস্বরূপ: 3/4 5/8

ধাপ 2. দ্বিতীয় ভগ্নাংশের অংক এবং হর উল্টো।

দ্বিতীয় ভগ্নাংশ এখন পারস্পরিক।

উদাহরণ: 3/4 8/5

ধাপ the. বিভাজনের প্রতীককে সময়ের প্রতীকে পরিবর্তন করুন।

একটি ভগ্নাংশ ভাগ করার জন্য, আপনি প্রথম ভগ্নাংশকে দ্বিতীয়টির পারস্পরিক দ্বারা গুণ করুন।

উদাহরণ: 3/4 x 8/5

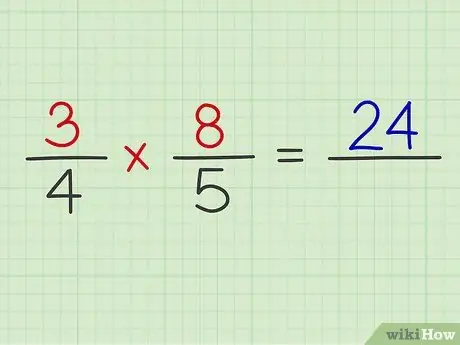
ধাপ 4. উভয় ভগ্নাংশের অংককে গুণ করুন।

শুধু দুটি নিয়মিত ভগ্নাংশ গুণ করার মত এটি করুন।

উদাহরণ: 3 x 8 = 24

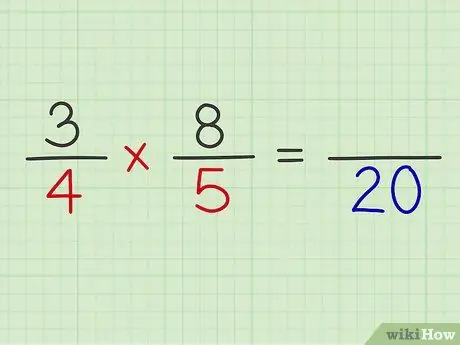
ধাপ 5. উভয় ভগ্নাংশের হর গুণ করুন।

দুটি ভগ্নাংশকে গুণ করে গণনা সম্পন্ন করুন।

উদাহরণ: 4 x 5 = 20

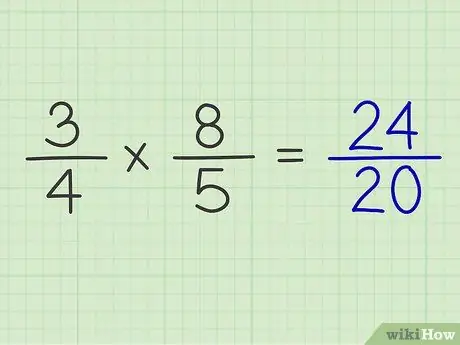
ধাপ den. হরের উৎপাদকের উপরে অঙ্কের গুণফল রাখুন।

দুটি ভগ্নাংশের অংক এবং হর গুণ করার পর, আপনি উভয় ভগ্নাংশ গণনার ফলাফল পেতে পারেন।

উদাহরণ: 3/4 x 8/5 = 24/20

ধাপ 7. সরলীকরণ ভগ্নাংশ।

গ্রেটেস্ট কমন ফ্যাক্টর, অথবা সংখ্যা এবং হরকে সমানভাবে ভাগ করা সবচেয়ে বড় সংখ্যা খুঁজে বের করা। এই ক্ষেত্রে, 24 এবং 20 এর সর্ববৃহৎ সাধারণ ফ্যাক্টর হল 4. এটি প্রমাণ করার জন্য, সমস্ত সংখ্যার এবং হরগুলি লিখুন এবং উভয়ের সর্ববৃহৎ সাধারণ কারণগুলির সংখ্যাকে বৃত্ত করুন।

• 24: 1, 2, 3, 4, 6, 8, 12, 24

• 20: 1, 2, 4, 5, 10, 20

  • যেহেতু 4 হল 24 এবং 20 এর সর্ববৃহৎ সাধারণ ফ্যাক্টর, তাই ভগ্নাংশটিকে সহজ করার জন্য দুটি সংখ্যাকে 4 দিয়ে ভাগ করুন।
  • 24/4 = 6
  • 20/4 = 5
  • 24/20 = 6/5

ধাপ 8. ভগ্নাংশটিকে একটি মিশ্র সংখ্যা (alচ্ছিক) হিসাবে পুনর্লিখন করুন।

কৌতুক, হর দ্বারা অংককে ভাগ করুন এবং ফলাফলটি একটি সম্পূর্ণ সংখ্যা হিসাবে লিখুন। তারপরে একটি নতুন সংখ্যার হিসাবে বিভাজনের অবশিষ্টাংশ লিখুন, এবং ভগ্নাংশের হর পরিবর্তন হয় না। যেহেতু 6 ভাগ করে 5 টি ফলাফল 1 এর মধ্যে 1 এর অবশিষ্টাংশের সাথে, সম্পূর্ণ সংখ্যা 1 লিখুন, তারপরে নতুন অংক 1, তারপর হর 5 একটি মিশ্র সংখ্যা 1 1/5 পেতে।

উদাহরণ: 6/5 = 1 1/5

5 এর 4 পদ্ধতি: বিভাজক সূচক

ধাপ 1. নিশ্চিত করুন যে সূচক/ক্ষমতা একই বেস নম্বর আছে।

আপনি শুধুমাত্র সূচকগুলি ভাগ করতে পারেন যদি তাদের একই বেস নম্বর থাকে। অন্যথায়, আপনি একই বেস নম্বর না পাওয়া পর্যন্ত আপনি তাদের ম্যানিপুলেট করার চেষ্টা করতে পারেন।

উদাহরণ: x⁸ এক্স⁵

ধাপ 2. সূচক বিয়োগ করুন।

আপনি কেবল দ্বিতীয় দ্বারা প্রথম সূচকটি বিয়োগ করতে পারেন। আপাতত বেস নাম্বার নিয়ে কিছু মনে করবেন না।

উদাহরণ: 8 - 5 = 3

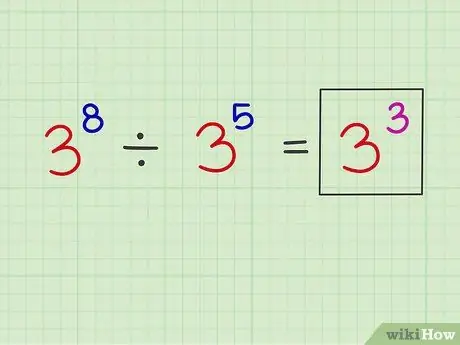
ধাপ the. মূল বেস নম্বরের উপরে নতুন সূচক রাখুন।

এখন, আপনি মূল বেস নম্বরের উপর নতুন সূচক লিখতে পারেন।

উদাহরণ: x⁸ এক্স⁵ = x³

5 এর পদ্ধতি 5: দশমিক সংখ্যা ভাগ করা

ধাপ 1. প্রশ্নগুলো লিখ।

বিভাজক বারের বাইরে হর (ভাগ করার সংখ্যা), এবং বিভাজক বারের ভিতরে সংখ্যার (ভাগ করার সংখ্যা) লিখুন। দশমিক ভাগে, আপনার লক্ষ্য হল একটি দশমিক সংখ্যাকে একটি পূর্ণ সংখ্যায় রূপান্তর করা।

উদাহরণ: 65.5.5

ধাপ 2. হরকে একটি পূর্ণ সংখ্যায় পরিবর্তন করুন।

0.5 থেকে 5, ওরফে 5, 0 পরিবর্তন করতে ডানদিকে দশমিক বিন্দুকে এক অঙ্কে স্লাইড করুন।

ধাপ the. হর হিসাবে একই সংখ্যার সংখ্যার দ্বারা দশমিক বিন্দু স্থানান্তর করে অংক পরিবর্তন করুন।

যেহেতু আপনি সংখ্যার দশমিক বিন্দুকে এক অঙ্কে ডানদিকে সরান যাতে এটি একটি সম্পূর্ণ সংখ্যা হয়ে যায়, হরের দশমিক বিন্দুটিও এক অঙ্কের ডানদিকে স্থানান্তরিত হয় যাতে 65.5 655 তে পরিবর্তিত হয়।

যদি আপনি সংখ্যার দশমিক বিন্দুকে তার সমস্ত অঙ্কের বাইরে স্থানান্তর করেন, এর অর্থ হল প্রতিবার দশমিক বিন্দু স্থানান্তরিত হলে আপনাকে অঙ্কগুলিতে শূন্য যোগ করতে হবে। উদাহরণস্বরূপ, যদি দশমিক বিন্দু 7, 2 কে তিনটি অঙ্কে ডানদিকে স্থানান্তরিত করা হয়, সংখ্যাটি 7,200 এ পরিবর্তিত হয় কারণ দুই অঙ্কের ফাঁকা স্থানটি শূন্যে ভরা।

ধাপ 4. সংখ্যার দশমিক বিন্দুর ঠিক উপরে লম্বা বিভাজন বারে দশমিক বিন্দু রাখুন।

যেহেতু আপনি দশমিক বিন্দুকে এক অঙ্কে স্থানান্তর করছেন 0.5 একটি পূর্ণ সংখ্যা, তাই দশমিক বিন্দুটিকে বিভাজন বারের ঠিক উপরে রাখা ভালো যেখানে দশমিক বিন্দু স্থানান্তরিত হয়, অর্থাৎ 655 -এ শেষ 5 -এর পরে।

ধাপ 5. সহজ দীর্ঘ বিভাজন দিয়ে সমস্যার সমাধান করুন।

655 কে 5 দিয়ে ভাগ করতে, পদক্ষেপগুলি হল:

• অঙ্কের শত অঙ্ক (6) হর (5) দ্বারা ভাগ করুন। ফলাফলটি 1 এর অবশিষ্টাংশ সহ 1।
• 1 এর বাকি অংশটি সংখ্যার দশ অঙ্কের (5) থেকে বিয়োগ করা হয় যাতে আপনি এখন 15 পান। 15 পেতে 5 দিয়ে ভাগ করুন 3 পেতে। বিভাজক বারের উপরে 3 লিখুন, 1 এর ডানদিকে।
• শেষ 5 টি সংখ্যা ফেলে দিন। 5 পেতে 5 দিয়ে ভাগ করুন 1. ভাজক বারের উপরে 1 নম্বরটি লিখুন, 3 নম্বরের ডানদিকে। কোন অবশিষ্ট নেই কারণ 5 5 দ্বারা বিভাজ্য।
• দীর্ঘ অনুক্রমিক বিভাজনের উত্তর 655 5 = 131। এই ফলাফল 65.5 0.5 প্রশ্নের উত্তরের সমান।