ভগ্নাংশ যোগ করা এবং বিয়োগ করা একটি গুরুত্বপূর্ণ দক্ষতা। দৈনন্দিন জীবনে ভগ্নাংশ সব সময় দেখা যায়, বিশেষ করে গণিতের ক্লাসে, প্রাথমিক থেকে কলেজ পর্যন্ত। সমান ভগ্নাংশ, অসম ভগ্নাংশ, মিশ্র সংখ্যা বা সাধারণ ভগ্নাংশ থেকে ভগ্নাংশ যোগ এবং বিয়োগ করতে শিখতে এই পদক্ষেপগুলি অনুসরণ করুন। আপনি যদি ইতিমধ্যেই একটি উপায় জানেন, তবে অন্যান্য ভগ্নাংশগুলি সমাধান করা সত্যিই সহজ!
ধাপ
4 এর মধ্যে পদ্ধতি 1: একই হরের সাথে ভগ্নাংশ যোগ করা এবং বিয়োগ করা
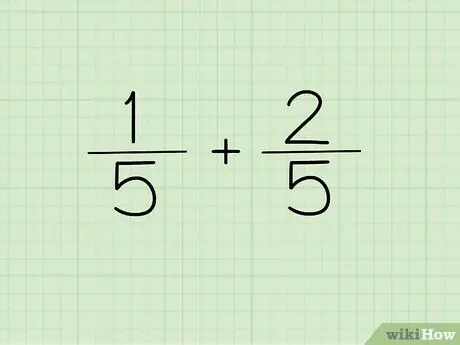
ধাপ 1. আপনার প্রশ্ন লিখুন।
যদি আপনি যে দুটি ভগ্নাংশকে যোগ বা বিয়োগ করতে চান তার হর যদি একই হয়, তাহলে আপনার উত্তরের হর হিসেবে একবার হরামটি লিখুন।
অন্য কথায়, 1/5 এবং 2/5 1/5 + 2/5 = লিখার প্রয়োজন নেই?, কিন্তু (1+2)/5 = হিসাবে লেখা যায়? । হরগুলি একই, তাই সেগুলি কেবল একবার লেখা যেতে পারে। দুটি অংক একত্রিত।
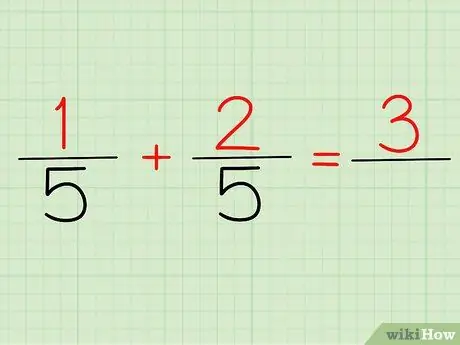
ধাপ ২. সংখ্যার যোগ করুন।
অংক হল সেই সংখ্যা যা যেকোন ভগ্নাংশের উপরে। যদি আমরা উপরের সমস্যাটি দেখি, 1/5 এবং 2/5, 1 এবং 2 হল আমাদের অংক।
আপনি এটি 1/5 + 2/5 বা (1 + 2)/5 লিখুন না কেন, আপনার উত্তর একই হবে: 3! কারণ, 1 + 2 = 3।
ধাপ the. হর ত্যাগ করুন।
যেহেতু হরগুলি একই, তাই হরদের সাথে কিছু করবেন না! যোগ, বিয়োগ, গুণ বা ভাগ করবেন না। এটা হতে দাও.
সুতরাং, একই উদাহরণ থেকে, আমাদের হর 5। ঠিক! 5 আমাদের ভগ্নাংশের নিচের সংখ্যা। আমরা অর্ধেক উত্তর পেয়েছি
ধাপ 4. আপনার উত্তর লিখুন।
এখন, আপনাকে যা করতে হবে তা হ'ল আপনার সংখ্যার এবং হরটি লিখুন! আপনি যদি উপরের উদাহরণটি ব্যবহার করেন, তাহলে আপনার উত্তর হবে 3/5।
আপনার অংক কত? 3. আপনার হর? 5. অতএব, 1/5 + 2/5 বা (1 + 2)/5 এর সমান 3/5.
4 এর পদ্ধতি 2: বিভিন্ন হরগুলির সাথে ভগ্নাংশ যোগ করা এবং বিয়োগ করা
ধাপ 1. সর্বনিম্ন সাধারণ হর খুঁজুন।
অর্থাৎ, ক্ষুদ্রতম হর দুটি ভগ্নাংশের জন্য একই। ধরুন আমাদের 2/3 এবং 3/4 ভগ্নাংশ আছে। হর কি? 3 এবং 4. উভয় ভগ্নাংশের সর্বনিম্ন সাধারণ হর খুঁজে পেতে, আপনি এটি তিনটি উপায়ে করতে পারেন:
- এর গুণক লিখ। 3 এর গুণক হল 3, 6, 9, 12, 15, 18… ইত্যাদি। 4 এর গুণক? 4, 8, 12, 16, 20, এবং তাই। ক্ষুদ্রতম সংখ্যাটি কী যা দুইটির একাধিক? 12! এটি সর্বনিম্ন সাধারণ হর।
-
আপনি উত্তর দিবেন. আপনি যদি ফ্যাক্টর সম্পর্কে জানেন, তাহলে আপনি প্রাইম ফ্যাক্টরাইজেশন করতে পারেন। অর্থাৎ, আপনি সেই সংখ্যাগুলি খুঁজছেন যা আপনার হরকে তৈরি করে। 3 নম্বরের জন্য, ফ্যাক্টর 3 এবং 1. 4 নম্বরের জন্য, ফ্যাক্টর 2 এবং 2. তারপর, আপনারা সবাই। 3 x 2 x 2 = 12. আপনার সর্বনিম্ন সাধারণ হর!
ছোট সংখ্যার জন্য সমস্ত সংখ্যা গুণ করুন। কিছু সমস্যার মধ্যে, এই মত, আপনি উভয় সংখ্যাকে গুণ করতে পারেন - 3 x 4 = 12. তবে, যদি আপনার একটি বড় হর থাকে তবে এটি করবেন না আপনি 56 x 44 কে গুণ করতে চান না এবং 2,464 পেতে সর্বস্বান্ত হন
ধাপ 2. ক্ষুদ্রতম সাধারণ হর পেতে প্রয়োজনীয় সংখ্যা দ্বারা হরকে গুণ করুন।
অন্য কথায়, আপনি আপনার সব হর সমান হতে চান। আমাদের উদাহরণে, আমরা হরটি 12 হতে চাই। 3 থেকে 12 পরিবর্তন করার জন্য, আপনি 3 কে 4 দিয়ে গুণ করুন। 4 থেকে 12 পরিবর্তন করার জন্য, আপনি 4 কে 3 দিয়ে গুণ করুন। একই হরটি আপনার চূড়ান্ত উত্তরের হর হবে।
-
সুতরাং 2/3 হয়ে যায় 2/3 x 4 এবং 3/4 হয়ে যায় 3/4 x 3. অর্থাৎ আমাদের এখন 2/12 এবং 3/12 আছে। কিন্তু, আমরা এখনো শেষ করিনি!
- আপনি লক্ষ্য করবেন যে হরগুলি একে অপরের দ্বারা গুণিত হয়। এই পরিস্থিতিতে এটি করা যেতে পারে, কিন্তু সব পরিস্থিতিতে নয়। কখনও কখনও, উভয় হরকে গুণ করার পরিবর্তে, আপনি ছোট সংখ্যা পেতে উভয় হরকে অন্য সংখ্যা দ্বারা গুণ করতে পারেন।
- তারপর অন্যান্য সমস্যাগুলিতে, কখনও কখনও আপনাকে কেবল একটি হরকে গুণ করতে হবে যাতে এটি সমস্যাটির অন্য ভগ্নাংশের হরের সমান হয়।
ধাপ the. একই সংখ্যা দ্বারা অংককে গুণ করুন।
যখন আপনি হরকে একটি সংখ্যা দ্বারা গুণ করেন, তখন আপনাকে অবশ্যই একই সংখ্যা দ্বারা সংখ্যাকেও গুণ করতে হবে। আমরা শেষ ধাপে যা করেছি তা কেবল গুণের অংশ যা করতে হবে।
আমাদের প্রথম ধাপ হিসেবে 2/3x4 এবং 2/4x3 আছে - তারপর, দ্বিতীয় ধাপে 2 x 4/3 x 4 এবং 3 x 3/4 x 3. অর্থাৎ আমাদের নতুন সংখ্যা 8/12 এবং 9/ 12। নিখুঁত
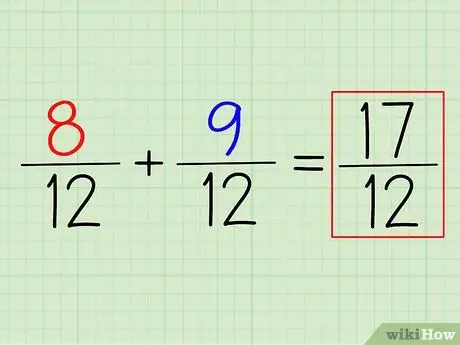
ধাপ 4. উত্তর পেতে সংখ্যার যোগ করুন (বা বিয়োগ করুন)।
8/12 + 9/12 যোগ করতে, আপনাকে যা করতে হবে তা হল সংখ্যার যোগ করা। মনে রাখবেন: কেবল হরটি ছেড়ে দিন। আপনি যে ক্ষুদ্রতম সাধারণ হর খুঁজে পাবেন তা হল আপনার চূড়ান্ত হর।
এই উদাহরণে, (8+9)/12 = 17/12। এটিকে একটি মিশ্র সংখ্যায় রূপান্তর করার জন্য, হর থেকে হরটি বিয়োগ করুন এবং বাকীটি লিখুন। এই ক্ষেত্রে, 17/12 = 1 5/12।
4 এর মধ্যে পদ্ধতি 3: মিশ্র এবং সাধারণ ভগ্নাংশ যোগ এবং বিয়োগ
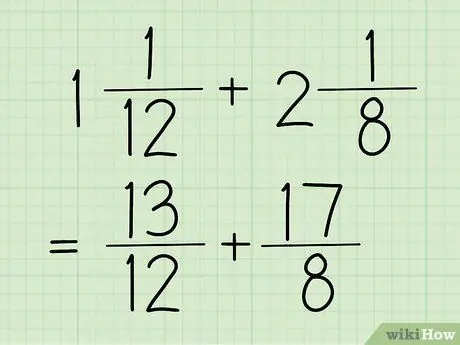
ধাপ 1. আপনার মিশ্র ভগ্নাংশগুলিকে সাধারণ ভগ্নাংশে রূপান্তর করুন।
একটি মিশ্র সংখ্যা হল একটি ভগ্নাংশ যার একটি পূর্ণ সংখ্যা এবং একটি ভগ্নাংশ, যেমন উপরের উদাহরণে (1 5/12)। এদিকে, একটি সাধারণ ভগ্নাংশ হল একটি ভগ্নাংশ যার সংখ্যার (শীর্ষ সংখ্যা) হর (নীচের সংখ্যা) এর চেয়ে বড়। এই ভগ্নাংশটি আগের ধাপেও দেখা যায়, যা 17/12।
এই বিভাগে উদাহরণের জন্য, আমরা 13/12 এবং 17/8 ব্যবহার করব।
পদক্ষেপ 2. একটি সাধারণ হর খুঁজুন।
সর্বনিম্ন সাধারণ হর খুঁজে পাওয়ার তিনটি উপায় মনে আছে? গুণক লেখার মাধ্যমে, প্রধান গুণক ব্যবহার করে, বা হরগুলিকে গুণ করে।
চলুন আমাদের উদাহরণের গুণক 12, 8 খুঁজে পাই। 24। 8, 16, 24, এবং 12, 24 - বিঙ্গো
ধাপ 3. সমান ভগ্নাংশ খুঁজে পেতে আপনার অংক এবং হর গুণ করুন।
উভয় হরকে 24 তে পরিবর্তন করতে হবে। আপনি কিভাবে 12 থেকে 24 রূপান্তর করবেন? 2. 8 থেকে 24? তিন দিয়ে গুণ করুন। কিন্তু ভুলে যাবেন না - আপনাকে সংখ্যাগুলিকেও গুণ করতে হবে!
সুতরাং (13 x 2)/(12 x 2) = 26/24। এবং (17 x 3)/(8 x 3) = 51/24। আমরা এটি প্রায় সম্পন্ন করেছি
ধাপ 4. আপনার ভগ্নাংশ যোগ করুন বা বিয়োগ করুন।
এখন যেহেতু আপনার একই হর আছে, আপনি সহজেই দুটি সংখ্যার যোগ করতে পারেন। মনে রাখবেন, শুধু হরিত ছেড়ে দিন!
26/24 + 51/24 = 77/24। এটাই তোমার যোগফল! যাইহোক, শীর্ষে সংখ্যাগুলি খুব বড় ছিল …
ধাপ ৫। আপনার উত্তরকে আবার মিশ্র সংখ্যায় রূপান্তর করুন।
ভগ্নাংশের শীর্ষে থাকা খুব বড় সংখ্যাটি কিছুটা অদ্ভুত মনে হয় - আপনি আপনার ভগ্নাংশের আকার বলতে পারবেন না। আপনাকে যা করতে হবে তা হ'ল সংখ্যার থেকে আপনার হরকে বারবার বিয়োগ করা যতক্ষণ না এটি আর বিয়োগ করা যায় এবং বাকীটি লিখুন।
-
এই উদাহরণে, 77 বিয়োগ 24 দ্বারা 3 গুণ। অর্থাৎ, 24 x 3 = 72. অবশিষ্ট 5! তাহলে আপনার শেষ ফলাফল কি? 3 5/24.
আসলেই সত্য!
4 এর পদ্ধতি 4: LCM না খুঁজে ভগ্নাংশ যোগ করুন এবং বিয়োগ করুন
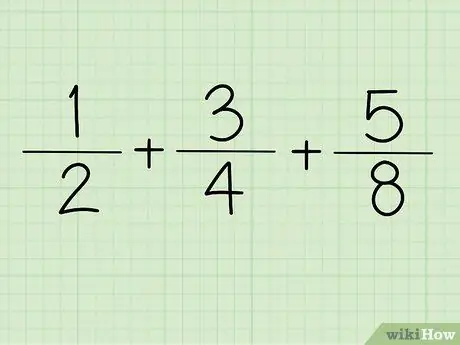
ধাপ 1. ভগ্নাংশটি লিখ।
উদাহরণস্বরূপ + +
ধাপ 2. প্রথমে অংকটি সমাধান করুন।
- অন্য ভগ্নাংশের অংক দ্বারা গুণ করুন।
- 1 এবং 4 দ্বারা গুণ করুন। [32]
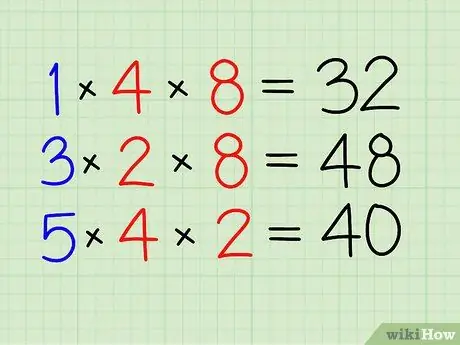
ধাপ 3. অন্যান্য ভগ্নাংশের জন্য একই করুন।
- 3 কে 2 এবং 8 দ্বারা গুণ করুন। [48]
- অবশেষে, 5 কে 4 এবং 2 দ্বারা গুণ করুন। [40]
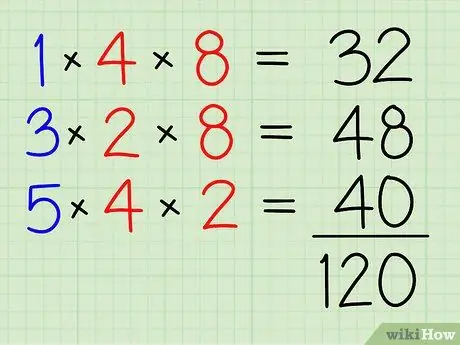
ধাপ 4. তাদের সব একসাথে যোগ করুন।
32+48+40=120
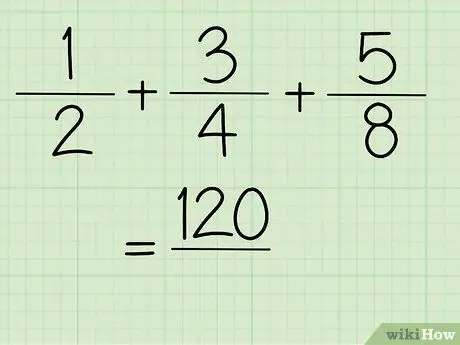
ধাপ 5. এখন, আপনি সংখ্যার মান পাবেন।
ধাপ 6. ভগ্নাংশের হরটি সমাধান করুন।
ধাপ 7. সমস্ত ভগ্নাংশের হর গুণ করুন।
2×4×8=64
ধাপ 8. এখন, আপনি ফলাফল পেতে।
120/64 = 1 56/64 = 1 ⅞
সতর্কবাণী
- এই পদ্ধতিটি আপনাকে বড় সংখ্যাগুলি গুণ করতে দেয়।
- এইভাবে হিসাব করার জন্য আপনার একটি ক্যালকুলেটর প্রয়োজন হতে পারে।
