সম্পূর্ণ সংখ্যা দ্বারা ভগ্নাংশ ভাগ করা যতটা কঠিন মনে হয় ততটা কঠিন নয়। একটি পূর্ণসংখ্যা দ্বারা একটি ভগ্নাংশ ভাগ করার জন্য, আপনাকে যা করতে হবে তা হল সম্পূর্ণ সংখ্যাটিকে একটি ভগ্নাংশে রূপান্তর করা, ভগ্নাংশের পারস্পরিক খুঁজে বের করা এবং ফলাফলটিকে প্রথম ভগ্নাংশ দ্বারা গুণ করা। আপনি কীভাবে এটি করতে চান তা জানতে চাইলে কেবল এই পদক্ষেপগুলি অনুসরণ করুন:
ধাপ
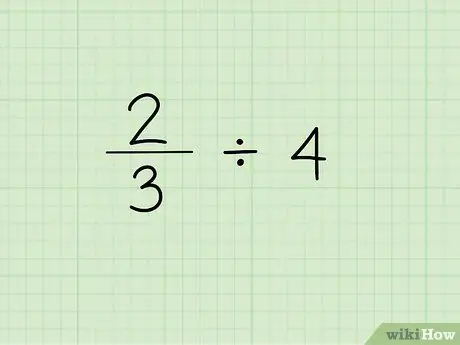
পদক্ষেপ 1. সমস্যাটি লিখুন।
একটি পূর্ণসংখ্যা দ্বারা একটি ভগ্নাংশ ভাগ করার প্রথম ধাপ হল ভগ্নাংশটি লিখুন তার পরে বিভাজন চিহ্ন এবং পূর্ণসংখ্যা যা আপনাকে ভগ্নাংশ ভাগ করতে হবে। ধরা যাক আমরা নিম্নলিখিত সমস্যা নিয়ে কাজ করছি: 2/3 4।
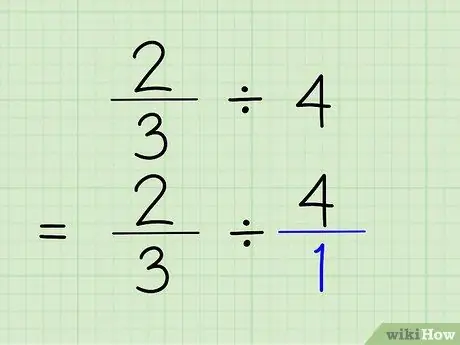
ধাপ 2. পূর্ণসংখ্যাকে ভগ্নাংশে রূপান্তর করুন।
একটি পূর্ণসংখ্যাকে একটি ভগ্নাংশে রূপান্তর করার জন্য, আপনাকে যা করতে হবে তা হল সংখ্যাটির উপরে পূর্ণসংখ্যা স্থাপন করতে হবে। 4/1 বলা আসলে 4 বলার মতই, কারণ আপনি কেবল দেখিয়েছেন যে সংখ্যাটিতে "1" 4 বার রয়েছে। সমস্যা হবে 2/3 4/1।
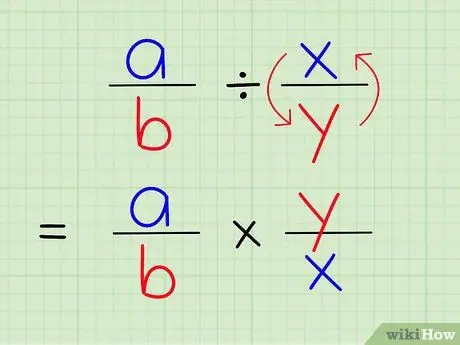
ধাপ a. একটি ভগ্নাংশকে অন্য দিয়ে ভাগ করা সেই ভগ্নাংশকে অন্য ভগ্নাংশের পারস্পরিক দ্বারা গুণ করার সমান।
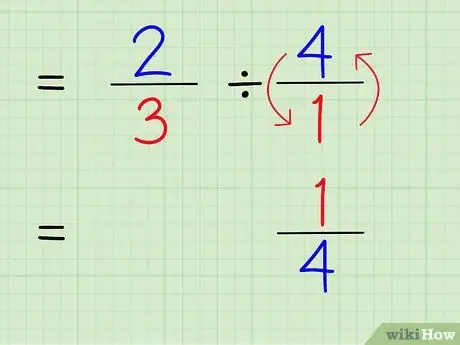
ধাপ 4. পূর্ণসংখ্যার পারস্পরিক লিখ।
একটি সংখ্যার পারস্পরিক খুঁজে বের করতে, সংখ্যার অংক এবং হর বদল করুন। অতএব, 4/1 এর পারস্পরিক খুঁজে বের করার জন্য, কেবল সংখ্যা এবং হরকে সোয়াপ করুন যাতে সংখ্যাটি 1/4 হয়।
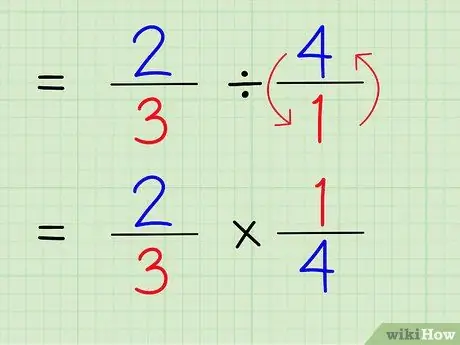
ধাপ 5. বিভাজন চিহ্নকে গুণিতক চিহ্নতে পরিবর্তন করুন।
সমস্যা হবে 2/3 x 1/4।
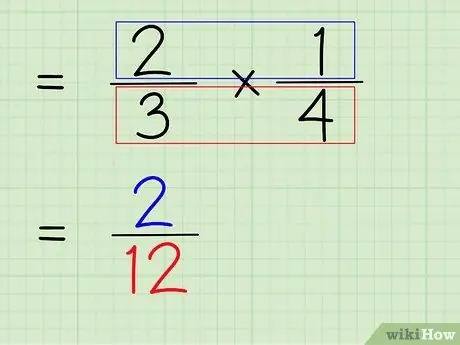
ধাপ 6. ভগ্নাংশের অংক এবং হরকে গুণ করুন।
সুতরাং, পরবর্তী ধাপ হল চূড়ান্ত উত্তর হিসাবে একটি নতুন অংক এবং হর পেতে ভগ্নাংশের অংক এবং হরকে গুণ করা।
- সংখ্যার সংখ্যাবৃদ্ধি করার জন্য, 2 পেতে 1 x 2 গুণ করুন।
- হরগুলিকে গুণ করতে, 12 পেতে 3 x 4 গুণ করুন।
- 2/3 x 1/4 = 2/12
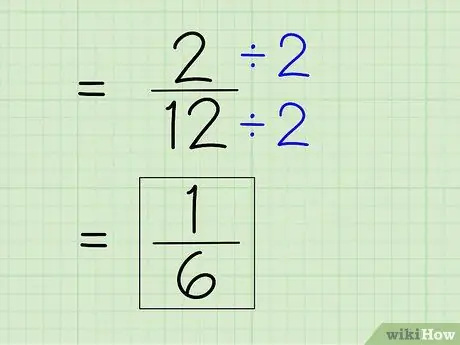
ধাপ 7. ভগ্নাংশ সরলীকরণ।
একটি ভগ্নাংশকে সরল করার জন্য, আপনাকে অবশ্যই ক্ষুদ্রতম হর খুঁজে বের করতে হবে, যার মানে হল যে আপনাকে সংখ্যা এবং হরকে যে কোন সংখ্যা দ্বারা ভাগ করতে হবে যা উভয় সংখ্যাকে ভাগ করে। যেহেতু 2 হল সংখ্যার, তাই আপনাকে দেখতে হবে যে 2 সম্পূর্ণভাবে 12 ভাগ করতে পারে - এটি করতে পারে কারণ 12 একটি সমান সংখ্যা। তারপরে, একটি সহজ উত্তর পেতে একটি নতুন অংক এবং হর পেতে 2 দ্বারা ভাগ এবং হর ভাগ করুন।
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- ভগ্নাংশ 2/12 সরলীকরণ করা যায় 1/6। এটি আপনার চূড়ান্ত উত্তর।
পরামর্শ
- এটি মেমোরিকে সহায়তা করার জন্য, এই সমস্ত গণনা কীভাবে করবেন তা মনে রাখার একটি সহজ উপায়। এটি মনে রাখবেন: "ভগ্নাংশ ভাগ করা, দ্বিতীয় সংখ্যা বিপরীত করা এবং গুণ করা সহজ!"
- উপরের পদ্ধতির আরেকটি প্রকরণ হল JGB/JBG। প্রথম সংখ্যা পরিবর্তন করবেন না। গুণে পরিবর্তন করুন। শেষ সংখ্যাটি বিপরীত করুন। অথবা প্রথমে বি তারপর জি।
- যদি আপনি গণনাটি গুন করার আগে বাতিল করেন, তাহলে আপনাকে ভগ্নাংশের সহজতম ফর্মটি খুঁজে বের করতে হবে না কারণ ফলাফলটি আপনি দেখতে পাচ্ছেন সহজ ভগ্নাংশ আকারে। আমাদের উদাহরণে, আমরা 2/3 × 1/4 গুণ করার আগে, আমরা দেখতে পাই যে প্রথম অংক (2) এবং দ্বিতীয় হর (4) এর একই গুণক 2, যা আমরা গণনা চালিয়ে যাওয়ার আগে বাতিল করতে পারি। এটি সমস্যাটিকে 1/3 × 1/2 এ রূপান্তরিত করে, যা তাৎক্ষণিক 1/6 ফলাফল দেয় এবং পরবর্তী পর্যায়ে ভগ্নাংশকে সরল করার সময় বাঁচায়।
- যদি আপনার একটি ভগ্নাংশ নেতিবাচক হয়, তবে এই পদ্ধতিটি এখনও কার্যকর; আপনি এই পদক্ষেপগুলি সম্পাদন করার সময় লক্ষণগুলির উপর নজর রাখুন তা নিশ্চিত করুন।
