যদিও নির্ভুলতা এবং নির্ভুলতা প্রায়শই বিনিময়যোগ্যভাবে ব্যবহৃত হয়, তারা আসলে গণিত এবং বিজ্ঞানের ক্ষেত্রে খুব আলাদা শব্দ। যথার্থতা মানে যে একটি পরিমাপ প্রতিবার এটি তৈরি করা হয় প্রায় একই মান আছে। উদাহরণস্বরূপ, যদি আপনি পরপর 5 বার স্কেলে পদার্পণ করেন, যে স্কেলে ভাল নির্ভুলতা রয়েছে সে প্রতিবার একই ভর দেখাবে। গণিত এবং বিজ্ঞানে, আপনার ডেটা এবং পরিমাপ সঠিক ডেটা পাওয়ার জন্য সঠিকভাবে কাজ করছে কিনা তা নির্ধারণ করতে নির্ভুলতা গণনা করা খুবই গুরুত্বপূর্ণ। ভাগ্যক্রমে, নির্ভুলতা গণনা করা বেশ সহজ।
ধাপ
ধাপ 1. নির্ভুলতা এবং নির্ভুলতার মধ্যে পার্থক্য জানুন।
যথার্থতা আপনার সরঞ্জামগুলি কতটা ভাল কাজ করে তা পরিমাপ করে না। সঠিকতা আপনার উত্তর কতটা সঠিক তা পরীক্ষা করে। উদাহরণস্বরূপ, যদি আপনার ভর 9 কেজি হয় এবং আপনার স্কেল 8.7 কেজি দেখায়, আপনার স্কেল সঠিক নয়। যদি আপনার স্কেল প্রতিবার আপনার ভর ওজন 8.7 কেজি দেখায়, তবে এটি এখনও সঠিক, যদিও সঠিক নয়।
এই তীরন্দাজ পদে দুটি শব্দ চিন্তা করুন: সঠিকতা আমরা যদি তীরন্দাজি লক্ষ্যবস্তু (ষাঁড়) গুলি প্রতিবার আমরা গুলি যথার্থতা যদি আমরা প্রতিবার গুলি করার সময় একই স্থানে আঘাত করি, এমনকি যদি সেই স্থানটি লক্ষ্যবস্তু না হয় যা আমরা আঘাত করতে চাই।
ধাপ 2. বিভিন্ন পরিমাপ রেকর্ড করুন।
নির্ভুলতা গণনা করার জন্য, আপনার কিছু সম্পর্কে তথ্য প্রয়োজন। উদাহরণস্বরূপ, যদি আপনি আপনার স্কেলের যথার্থতা পরীক্ষা করতে চান, তাহলে আপনি এটিতে দাঁড়াতে পারেন এবং স্কেলে প্রদর্শিত সংখ্যাটি 15 বার রেকর্ড করতে পারেন।
নির্ভুলতা গণনা করার জন্য আপনাকে একই অবস্থার অধীনে একই বস্তুর একাধিক পরিমাপ রেকর্ড করতে হবে। আপনি 10 জন ভিন্ন ব্যক্তির ওজন করতে পারবেন না এবং ফলাফলগুলি তুলনা করতে পারবেন না।
ধাপ 3. আপনার ডেটার গড় বা গড় খুঁজুন।
নির্ভুলতার পরিবর্তন লক্ষ্য করার জন্য, আপনাকে আপনার ডেটাকে কোন কিছুর সাথে তুলনা করতে হবে। গড় বা গড় আপনার ডেটার কেন্দ্র বিন্দু এবং এটি একটি ভাল মানদণ্ড। গড় খুঁজে পেতে, আপনার নেওয়া সমস্ত পরিমাপ যোগ করুন এবং আপনার নেওয়া পরিমাপের সংখ্যা দ্বারা সংখ্যাটি ভাগ করুন। যদি, আপনার ভর ওজন করার সময়, আপনি ভর রেকর্ড করেন: 12 কেজি, 11 কেজি, 14 কেজি, 13 কেজি এবং 12 কেজি, আপনার গড় হবে:
(12 কেজি + 11 কেজি + 14 কেজি + 13 কেজি + 12 কেজি) / 5 = 62/5 = 12.4 কেজি
। অন্য কথায়, গড় ভর রেকর্ড করা হয় 12.4 কেজি.
আপনি এমন সংখ্যাগুলিও ব্যবহার করতে পারেন যা আপনি ইতিমধ্যে জানেন এবং গড় ব্যবহার করার প্রয়োজন নেই। উদাহরণস্বরূপ, আপনি 10 কেজি আলুর ব্যাগ ব্যবহার করতে পারেন এবং এই সংখ্যার সাথে আপনার পরিসংখ্যান তুলনা করতে পারেন।
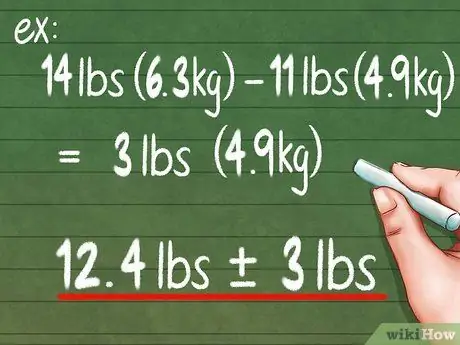
ধাপ 4. সহজ নির্ভুলতা গণনার জন্য স্ট্যান্ডার্ড রেঞ্জ ব্যবহার করুন।
পরিসীমা নির্ভুলতা নির্ধারণের সবচেয়ে সহজ উপায়। এটি গণনা করার জন্য, শুধু আপনার সর্বোচ্চ স্কোর নিন এবং সেই সর্বোচ্চ স্কোর থেকে আপনার সর্বনিম্ন স্কোর বিয়োগ করুন। উপরের উদাহরণের জন্য, 14 কেজি - 11 কেজি = 3 কেজি। তাই আপনি রিপোর্ট করতে পারেন যে বস্তুটি আপনি পরিমাপ করছেন 12.4 কেজি ± 3 কেজি
- ± 3 কেজির মান হল আপনার নির্ভুল পরিমাপ। এর মানে হল যে এই স্কেল মাত্র 6 কেজি বা 3 কেজি ভারী এবং 3 কেজি লাইটারের মধ্যে সুনির্দিষ্ট।
- ± প্রতীকটি "কমবেশি" হিসাবে পড়া যেতে পারে।
- নির্ভুলতা গণনার জন্য এই পদ্ধতিটি সর্বাধিক ব্যবহৃত পদ্ধতি। যদিও সহজ, বিদ্রূপাত্মকভাবে এই পদ্ধতিটি খুব সুনির্দিষ্ট নয়।
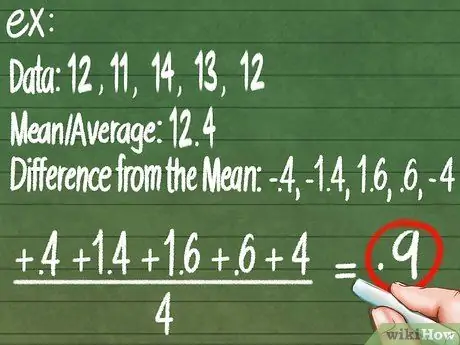
ধাপ ৫। আরো সুনির্দিষ্ট নির্ভুলতার জন্য গড় পরম বিচ্যুতি গণনা করুন।
আমাদের ডেটার মানে আবার দেখুন: 12.4 কেজি। ডেটা সেন্টার থেকে প্রতিটি পরিমাপ কতদূর তা খুঁজে বের করতে গড় থেকে প্রতিটি পরিমাপ বিয়োগ করুন। সমস্ত নেতিবাচক সংখ্যাকে ইতিবাচক করুন। উদাহরণ স্বরূপ:
তথ্য:
12, 11, 14, 13, 12. গড়/গড়:
12, 4
গড় থেকে পার্থক্য:
-0, 4; -1, 4; 1, 6; 0, 6; -0, 4"
। এখন, কেন্দ্র থেকে প্রতিটি পরিমাপের গড় কত দূরে তা খুঁজে পেতে এই সংখ্যার গড় খুঁজুন:
(0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4) / 5 = 0, 88 । এর মানে হল যে সাধারণভাবে আপনি যে পরিমাপ গ্রহণ করেন তা আপনি যা দেখেন তার থেকে ± 0.88 কেজি আলাদা হতে পারে।
আপনাকে অবশ্যই নেতিবাচক চিহ্নটি উপেক্ষা করতে হবে অন্যথায় মানগুলি একে অপরকে বাতিল করে দেবে। মনে রাখবেন যে 11, 4 এবং 13, 4 উভয়ই 12, 4 এর গড় থেকে 1 কেজি পার্থক্য, শুধুমাত্র পার্থক্যটি বিপরীত (ইতিবাচক বা নেতিবাচক)।
পরামর্শ
- যদি আপনার পরীক্ষার মানগুলির মধ্যে একটি অন্যদের চেয়ে বেশি বা কম হয়, তাহলে এই সংখ্যাটিকে আপনার গণনা থেকে বাদ দেবেন না। এমনকি যদি এই মানটি একটি ত্রুটি হয়, এটি ডেটা এবং সঠিক গণনার জন্য ব্যবহার করা উচিত।
- আরও সঠিক গণনা করার জন্য 5 টিরও বেশি চেষ্টা করুন। আপনি যত বেশি পরীক্ষা -নিরীক্ষা করবেন, স্পষ্টতা তত স্পষ্ট হবে।
